The derivative of xe-x is equal to (1-x)e-x. In this post, we will find the derivative of xe^-x by the product rule and the first principle of derivatives.
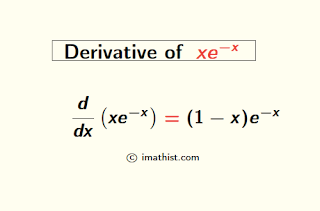
Derivative of xe-x by First Principle
The derivative of $f(x)=xe^{-x}$by the first principle is given by
$(xe^{-x})’$ = limh→0 $\dfrac{(x+h)e^{-(x+h)}-xe^{-x}}{h}$
= limh→0 $\dfrac{xe^{-(x+h)}+he^{-(x+h)}-xe^{-x}}{h}$
= limh→0 $\big(\dfrac{xe^{-(x+h)}-xe^{-x}}{h}$ $+\dfrac{he^{-(x+h)}}{h} \big)$
= limh→0 $\dfrac{xe^{-x}e^{-h}-xe^{-x}}{h}$ + limh→0 $e^{-(x+h)}$
= xe-x limh→0 $\dfrac{e^{-h}-1}{h}$ $+e^{-(x+0)}$
= xe-x limh→0 $\dfrac{e^{-h}-1}{-h} \times (-1)$ +e-x
Let z=-h. Then z →0 as h →0.
= -xe-x limh→0 $\dfrac{e^{z}-1}{z}$ $+e^{-x}$
= -xe-x ⋅ 1 +e-x as we know that the limit of (ez-1)/z tends to 1 when z tends to 0.
= -xe-x +e-x = (1-x)e-x.
Hence, the derivative of xe-x from the first principle is equal to (1-x)e-x.
Derivative of xe-x by Product Rule
Product rule of derivatives says that if f(x) = g(x) h(x) is a product of two functions, then the derivative of f(x) is given by
$\dfrac{d}{dx}(f(x))$ $=g(x) \dfrac{d}{dx}(h(x))+h(x) \dfrac{d}{dx}(g(x))$
We have f(x)=xe-x.
Take g(x)=x and h(x)=e-x in the product rule.
Thus, the derivative of f(x)=xe-x by the product rule is equal to
$\dfrac{d}{dx}(xe^{-x})$ $=x \dfrac{d}{dx}(e^{-x})+e^{-x} \dfrac{d}{dx}(x)$
= – xe-x +e-x ⋅ 1
= (1-x)e-x
Hence, the derivative of xe-x by the product rule is (1-x)e-x.
Also Read:
Derivative of root x + 1 by root x
FAQs
Q1: What is the derivative of xe-x?
Answer: The derivative of xe-x is equal to (1-x)e-x.