The cube root of x is an algebraic function. In this article, we will learn its definition, graph, various properties, etc. We will also learn how to find its derivative and integration.

Cube Root Definition
If A3 =x, then the number A is called a cube root of x. Symbolically, we can write it as
Note: The cube root of x can be written as x1/3, that is, 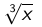 = x1/3.
= x1/3.
Cube Root Example
As 23 =8, by the above definition, we can say that 2 is a cube root of 8. More examples of cube roots are given below:
- As 33=27 , the number 3 is a cube root of 27.
- As 43 =64, the number 4 is a cube root of 64.
- As 53 =125, the number 5 is a cube root of 125.
Cube Root Graph
Taking cubes on both sides, we get that
y3 =x.
The graph of cube root is plotted below:

Source: Wikipedia
Cube Root Properties
Below are the properties of cube roots:
- The product of the cube roots of two numbers is the same as the cube root of the product of those two numbers. That is,

- If $a, b (\neq 0)$ be two real numbers. Then we have

- Cube root of a perfect cube is always an integer. Perfect cube is such a number that is the cube of some integer. For example, the cube root of $8$ is $2$, so $8$ is a perfect cube number.
- The cube root of 0 is 0.
- The cube roots of 1 are 1, ω, ω2, where ω=$\dfrac{-1 \pm \sqrt{3}i}{2}$.
- The cube root function is an odd function.
Cube Root Derivative
To find the derivative of cube root x, we will use the power rule: $\dfrac{d}{dx}(x^n)=nx^{n-1}$. We know that cube root of $x$ can be written as $x^{1/3}$.
$\dfrac{d}{dx}(x^{1/3})$
$=\dfrac{1}{3} x^{1/3-1}$
$=\dfrac{1}{3} x^{-2/3}$
So the derivative of cube root x is 1/3 x^{-2/3}.
Cube Root Integration
To find the integration of root x, we will use the power rule of integration: $\int x^n dx=\dfrac{x^{n+1}}{n+1}$.
$\int x^{1/3} dx$
$=\dfrac{x^{1/3 +1}}{1/3+1}$
$=\dfrac{x^{4/3}}{4/3}$
$=\dfrac{3}{4} x^{4/3}$
$=\dfrac{3}{4} x \cdot x^{1/3}$
$=\dfrac{3}{4} x\sqrt[3]{x}$
So the integration of root x is $\dfrac{3}{4} x\sqrt[3]{x}$.