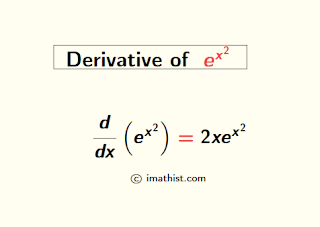Derivative of e^x^2 by First Principle and Chain Rule

The function e to the power x² is written as $e^{x^2}$ and its derivative is $2xe^{x^2}$. In this post, we will find the derivative of e to the power x square by the first principle and chain rule of derivatives.

Recall the first principle of derivatives: The derivative of a function f(x) by first principle is defined by the limit:

$\dfrac{d}{dx}(f(x))$ = lim_h→0 $\dfrac{f(x+h)-f(x)}{h}$ $\cdots$ (I)

We will use this to find the differentiation of e to the power x².

Derivative of $e^{x^2}$ by First Principle

Let us put $f(x)=e^{x^2}$ in the above formula (I).

So we obtain that

$\dfrac{d}{dx}(e^{x^2})$ = lim_h→0 $\dfrac{e^{(x+h)^2}-e^{x^2}}{h}$

= lim_h→0 $\dfrac{e^{x^2+2xh+h^2}-e^{x^2}}{h}$. Here we have used the formula (a+b)² = a²+2ab+b².

= lim_h→0 $\dfrac{e^{x^2}e^{2xh+h^2}-e^{x^2}}{h}$

= lim_h→0 $\dfrac{e^{x^2}(e^{2xh+h^2}-1)}{h}$

= lim_h→0 $\dfrac{e^{x^2}(e^{h(2x+h)}-1)}{h}$

= lim_h→0 $[\dfrac{e^{x^2}(e^{h(2x+h)}-1)}{h(2x+h)}$ $\times (2x+h) ]$

$=e^{x^2}\lim\limits_{h \to 0}$ $\dfrac{e^{h(2x+h)}-1}{h(2x+h)}$ $\times \lim\limits_{h \to 0} (2x+h)$

Let u=h(2x+h). Then u tends to zero when h tends to 0.

$=e^{x^2}\lim\limits_{u \to 0}$ $\dfrac{e^{u}-1}{u}$ $\times \lim\limits_{h \to 0} (2x+h)$

$=e^{x^2} \times 1$ $\times (2x+0)$ as the limit of (e^x-1)/x is 1 when x tends to 0.

$=2xe^{x^2}$

Thus, the derivative of e^x^2 by first principle is 2xe^x^2.

Derivative of $e^{x^2}$ by Chain Rule

Let u=x².

Then $\dfrac{du}{dx}=2x$.

Now, the derivative of $e^{x^2}$ by the chain rule is equal to

$\dfrac{d}{dx}(e^{x^2})$ $=\dfrac{d}{dx}(e^u)$

$= \dfrac{d}{du}(e^u) \cdot \dfrac{du}{dx}$

$=e^u \cdot 2x$ as du/dx=2x.

$=2xe^{x^2}$ as u=x².

Therefore, the differentiation of e to the power x² is equal to the product of 2x and e^{x^2}.

Also Read: 

Derivative of 1 by root(x)

Derivative of root x + 1 by root x

Derivative of x root(x)

Derivative of x sin(x)

Derivative of sin²(x)

Derivative of cos²(x)

FAQs