Integration of root(x)+1/root(x) | Anti Derivative of √x+1/√x

The integration of root x + 1/root x is equal to 2/3 x^3/2+2√x+C where C is an integral constant. In this post, we will learn how to integrate √x+1/√x.

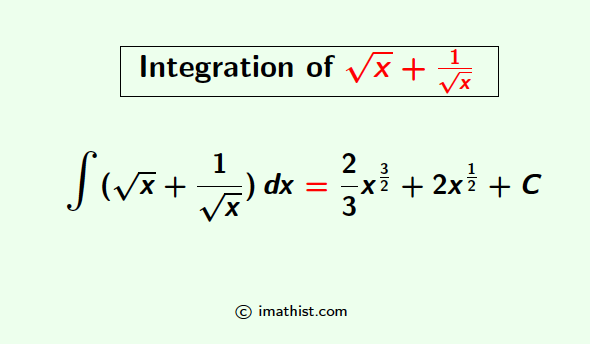
Integral of √x+1/√x

Question: Find the integral $\int (\sqrt{x}+\dfrac{1}{\sqrt{x}})\ dx$

Answer:

$\int (\sqrt{x}+\dfrac{1}{\sqrt{x}})\ dx$ = $\int \sqrt{x}\ dx$ + $\int \dfrac{1}{\sqrt{x}}\ dx$ by the sum rule of integration.

= ∫ x^1/2 dx + $\int \dfrac{1}{x^{1/2}}\ dx$

= ∫ x^1/2 dx + ∫ x^-1/2 dx

= $\dfrac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}$ + $\dfrac{x^{-\frac{1}{2}+1}}{-\frac{1}{2}+1}$ using the power rule of integration: $\int x^n dx =\dfrac{x^{n+1}}{n+1}$

= $\dfrac{x^{3/2}}{3/2}$ + $\dfrac{x^{1/2}}{1/2}$ + C where C is an integration constant.

= $\dfrac{2}{3} x^{3/2}$ $+2 \sqrt{x}$ + C

= $\dfrac{2}{3} x\sqrt{x}$ $+2 \sqrt{x}$ + C as we have $x^{3/2}=x\sqrt{x}$ by the power rule of indices.

So the integral of √x+1/√x is equal to $\dfrac{2}{3} x\sqrt{x}$ $+2 \sqrt{x}$ + C where C is an integration constant.

ALSO READ:

Integration of tanx

Integration of cotx

Integration of secx

Integration of cosecx

Integration of (ax+b)/(cx+d)

FAQ