sinx siny Formula | sinx siny Identity

The function sinx siny is the product of two sine functions sinx and siny. The formula or the identity of sinx siny is given as follows:

sinx siny = $\dfrac{\cos(x-y)-\cos(x+y)}{2}$

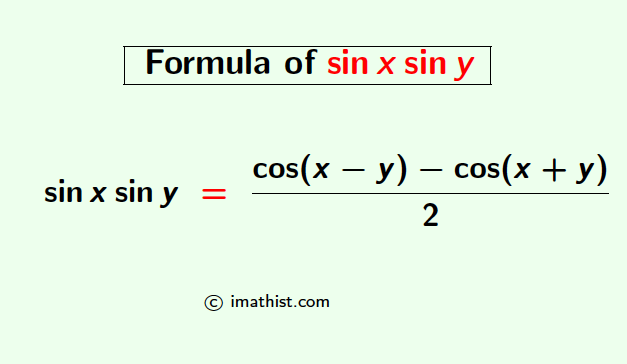
Proof of sinx siny Formula

We will now prove the sinx siny formula

sinx siny = $\dfrac{\cos(x-y)-\cos(x+y)}{2}$

Proof:

We know that

cos(x+y) = cosx cosy – sinx siny …(I)

cos(x-y) = cosx cosy + sinx siny …(II)

Subtracting (I) from (II), that is, doing (II)-(I), we get that

cos(x-y) – cos(x+y) = (cosx cosy + sinx siny) – (cosx cosy – sinx siny)

⇒ cos(x-y) – cos(x+y) = cosx cosy + sinx siny – cosx cosy + sinx siny

⇒ cos(x-y) – cos(x+y) = 2 sinx siny

⇒ sinx siny = $\frac{1}{2}$ [cos(x-y) – cos(x+y)]

Thus, sinx siny formula is given by sinx siny= 1/2 [cos(x-y) – cos(x+y)].

sinx siny Formula:

$\sin x \sin y = \dfrac{\cos(x-y)-\cos(x+y)}{2}$

ALSO READ:

sinx cosy Formula | cosx siny Formula

cosx cosy Formula | 1-sin²x Formula

Sin3x Formula in terms of sinx

Cos3x Formula in terms of cosx

Sin³x Formula | Cos³x Formula

Application of sinx siny Formula

Question 1: Find the value of sin45 sin15.

Answer:

Applying the above formula with x=45 and y=15, we obtain that

sin45 sin15 = $\dfrac{\cos(45-15)-\cos(45+15)}{2}$

= $\dfrac{\cos 30-\cos 60}{2}$

= $\dfrac{\frac{\sqrt{3}}{2} – \frac{1}{2}}{2}$

= $\dfrac{\frac{\sqrt{3}-1}{2}}{2}$

= $\dfrac{\sqrt{3}-1}{4}$

Hence the value of sin45 sin15 is equal to (√3-1)/4. We get this value by applying the sinx siny formula.

FAQs