The general solutions of sinx=-1 are given by x=(4n-1)π/2 where n is any integer. In this post, we will learn how to find the general solutions of the trigonometric equation sinx=-1.
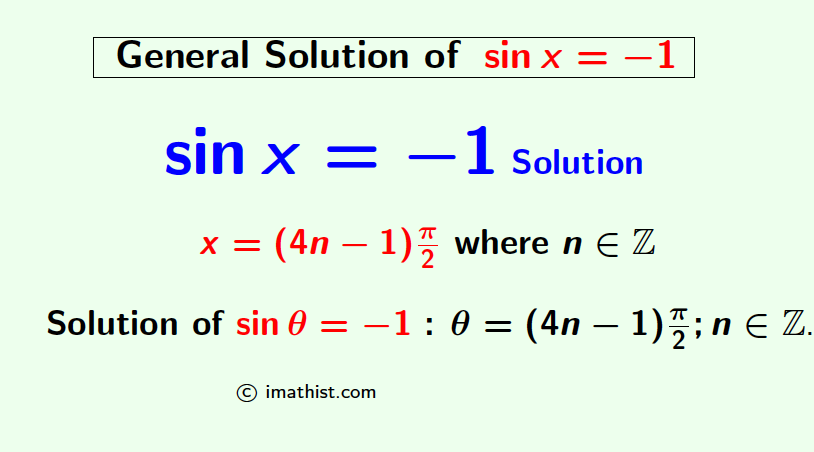
sinx=-1 General Solution
Question: Find the general solutions of sinx= -1.
Answer:
As sin(-π/2)= -1, the equation sinx= -1 can be written
sinx = sin(-π/2).
∴ x=mπ+(-1)m $(-\frac{\pi}{2})$ for some integers m. [Since the general solutions of sinθ = sinα are given by θ = nπ+(-1)n α, n ∈ Z.]
Case 1: First assume that m is even, that is, m=2n where n is an integer. So
x=2nπ+(-1)2n $(-\frac{\pi}{2})$
= 2nπ-$\frac{\pi}{2}$
= (4n-1)$\frac{\pi}{2}$ …(I)
Case 2: Next, assume that m is odd, that is, m=2n+1 for some integer n. So
x=(2n+1)π+(-1)2n+1 $(-\frac{\pi}{2})$
= (2n+1)π+$\frac{\pi}{2}$
= 2nπ+$\frac{3\pi}{2}$
= (4n+3)$\frac{\pi}{2}$ …(II)
Combining (I) and (II), we deduce that x=(4n-1)π/2.
So the general solution of sinx=1 equals x=(4n-1)π/2 where n is any integer. As n can be any integer, so sinx=-1 has infinite solutions.
Let us now find the general solutions of sin2x=-1 as an application of the general solution of sinx=-1.
sin2x=-1 General Solution
Question: Find the general solutions of sin2x= -1.
Answer:
From the above, we know that the general solutions of sinθ=-1 are given by θ=(4n-1)π/2 where n ∈ Z.
So the general solutions of sin2x=-1 are equal to
2x = (4n-1)π/2 where n ∈ Z.
⇒ x = (4n-1)π/4.
So the general solutions of sin2x= -1 are given by x=(4n-1)π/4 where n is an integer.
ALSO READ:
| tanx=tany General Solution | x=nπ+y; n ∈ Z |
| sinx=0 General Solution | x=nπ; n ∈ Z |
| sinx=1 General Solution | x=(4n+1)π/2; n ∈ Z |
FAQs
Q1: What are the general solutions of sinx=-1?
Answer: The general solutions of sinx=-1 are given by x=(4n-1)π/2 where n is an integer.
Q2: What are the general solutions of sinθ=-1?
Answer: The general solutions of sinθ=-1 are given by θ=(4n-1)π/2 where n ∈ Z.
Q3: What are the general solutions of sin2x=-1?
Answer: The general solutions of sin2x=-1 are given by x=(4n-1)π/4 where n is an integer.