The integration of sin^3x cos^2x is equal to (cos5x)/5 – (cos3x)/3 +C where C is a constant. Here we learn how to integrate sin^3x cos^2x.
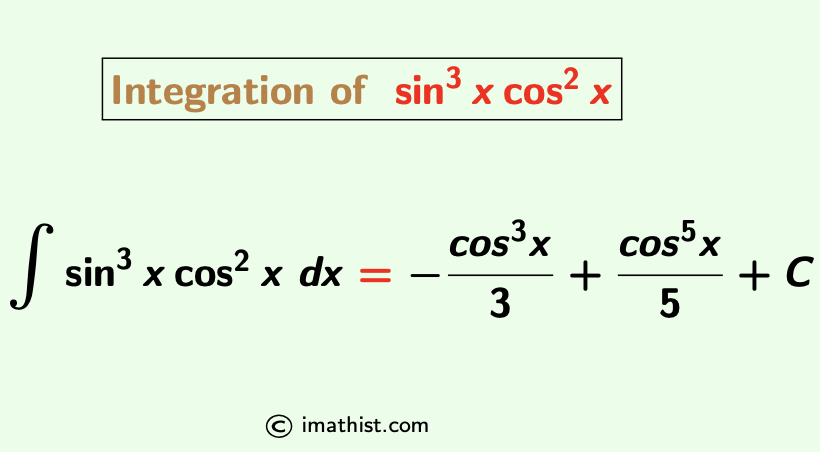
What is the Integration of sin3x cos2x?
Question: Find the integral of sin3x cos2x, that is,
Find ∫sin3x cos2x dx
Solution:
We have:
∫sin3x cos2x dx = ∫sin2x sin x cos2x dx
⇒ ∫sin3x cos2x dx = ∫(1 -cos2x) cos2x sin x dx [by the formula sin2x = 1 -cos2x]
Put cosx =z, so that -sinx dx =dz.
∴ From above, we have that
∫sin3x cos2x dx = – ∫(1 – z2) z2 dz
= – ∫(z2 – z4) dz
= – ∫z2 dz + ∫z4 dz
= – z3/3 + z5/5 +C
= – cos3x/3 + cos5x/5 +C
So the integration of sin3x cos2x equals to – cos3x/3 + cos5x/5 +C, that is, the integral of sin cube x cos square x is given by the formula:
| ∫sin3x cos2x dx = – cos3x/3 + cos5x/5 +C |
Related Integrals:
FAQs
Q1: What is the integral of sin^3x cos^2x?
Answer: The integration of sin^3x cos^2x is given by ∫sin3x cos2x dx = – cos3x/3 + cos5x/5 +C where C denotes an integral constant.