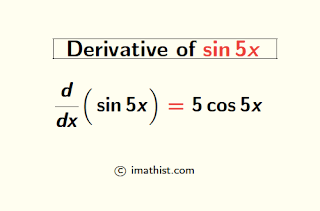Find the Derivative of sin5x [by First Principle]

The derivative of sin5x is equal to 5cos5x.  In this post, we will find the derivative of sin5x by the first principle, that is, by the limit definition of derivatives.

By the first principle of derivatives, we know that the derivative of a function f(x) is given by the following limit:

${\displaystyle \frac{d}{dx}}(f(x))$$=\underset{h\to 0}{lim}{\displaystyle \frac{f(x+h)-f(x)}{h}}$ …(I)

Derivative of sin5x by First Principle

Question: What is the derivative of $\sin 5x$?

Answer: The derivative of sin5x is 5cos5x.

Explanation:

Step 1: We put $f(x)=\sin 5x$ in the above formula (I).

Step 2: Thus the derivative of sin5x by the first principle will be equal to

${\displaystyle \frac{d}{dx}}(\sin 5x)$$=\underset{h\to 0}{lim}{\displaystyle \frac{\sin 5(x+h)-\sin 5x}{h}}$

Step 3: Applying the formula $\sin a-\sin b$ $=2\cos {\displaystyle \frac{a+b}{2}}\sin {\displaystyle \frac{a-b}{2}}$, we obtain that

${\displaystyle \frac{d}{dx}}(\sin 5x)$$=\underset{h\to 0}{lim}{\displaystyle \frac{1}{h}}\cdot 2\cos {\displaystyle \frac{10x+5h}{2}}\sin {\displaystyle \frac{5h}{2}}$

= $\underset{h\to 0}{lim}5\cdot \cos {\displaystyle \frac{10x+5h}{2}}\cdot {\displaystyle \frac{\sin {\displaystyle \frac{5h}{2}}}{{\displaystyle \frac{5h}{2}}}}$

= $5\underset{h\to 0}{lim}\cos {\displaystyle \frac{10x+5h}{2}}$ $\times \underset{h\to 0}{lim}{\displaystyle \frac{\sin {\displaystyle \frac{5h}{2}}}{{\displaystyle \frac{5h}{2}}}}$

[Let $z={\displaystyle \frac{5h}{2}}$. Then $z\to 0$ as $h\to 0$]

= $5\cos {\displaystyle \frac{10x+5\cdot 0}{2}}$ $\times \underset{z\to 0}{lim}{\displaystyle \frac{\sin z}{z}}$

= $5\cos 5x\cdot 1$ as the limit of sinx/x is 1 when x tends to zero.

= $5\cos 5x$.

Conclusion: Therefore, the derivative of sin5x is 5cos5x, obtained by the first principle of derivatives.

RELATED TOPICS:

Derivative of cos(e^x)

Derivative of sin⁵ x

Derivative of log(3x)

Derivative of e^1/x

Question-Answer on Derivative of sin5x

Question: What is the derivative of sin5x at x=0.

Answer: From the above, we have obtained that the derivative of sin5x is 5cos5x. So the derivative of sin5x at x=0 is equal to

$[{\displaystyle \frac{d}{dx}}(\sin 5x)]x=0$

$=[5\cos 5x]x=0$

$=5\cos 0$

$=5\cdot 1$ as the value of cos0 is 1.

$=5$.

Thus, the derivative of sin5x at x=0 is equal to 5.

FAQs