Sin3x formula in terms of cosx is expressed as follows: sin3x = (4cos2x-1)√(1-cos2x). Here we learn how to prove sin3x formula in terms of cosine of x.
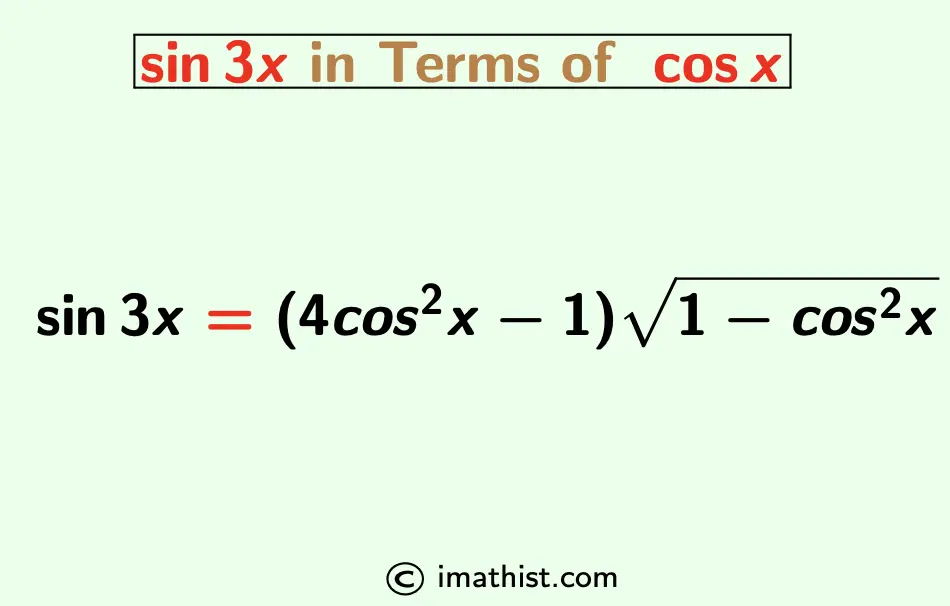
sin3x in Terms of cos x
In order to express sin3x formula in terms of cosx, we will use the following trigonometric formulae:
- sin(a+b) = sin a cos b +cos a sin b
- sin 2a=2sin a cos a
- cos 2a = 2cos2a -1
Using the above formulas, we obtain the formula of sin3x in terms of cosx as follows:
sin3x
= sin(2x+x)
= sin2x cos x +cos2x sin x by the above formula (1)
= (2sin x cos x) cos x +(2cos2x- 1) sin x by the above formulas (2) and (3).
= 2cos2x sinx + 2cos2x sinx – sinx
= 4cos2x sinx – sinx
= (4cos2x -1) sinx
= (4cos2x -1) $\sqrt{1-\cos^2 x}$
Therefore, the formula of sin 3x in terms of cosx is given by sin3x = (4cos2x-1)√(1-cos2x).
Have You Read These?
| Sin3x in terms of sinx |
| Cos3x in terms of sinx, cosx |
| Tan2x in terms of tanx, sinx, cosx |
| How to Simplify sin(cos-1x) |
FAQs
Q1: What is the sin3x formula in terms of cosx?
Answer: The sin3x formula in terms of cosx is given by sin3x = (4cos2x-1)√(1-cos2x).