The Laplace transform of t is equal to L{t} = 1/s2. Here we will find the Laplace of t by the definition of Laplace transforms.
The formula of the Laplace of t is given as follows:
L{t} = $\dfrac{1}{s^2}$.
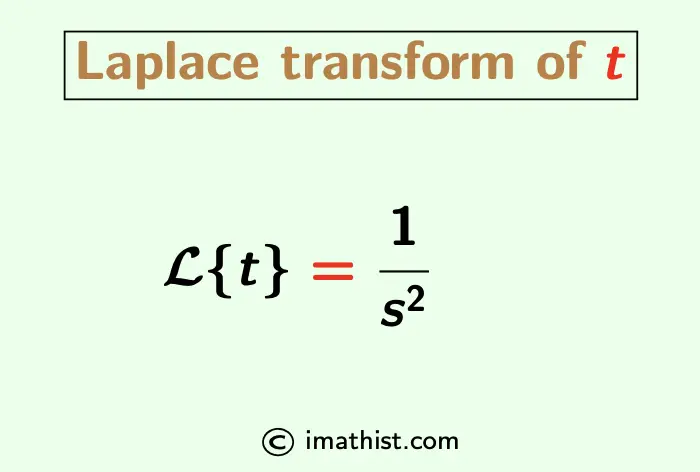
Find Laplace Transform of t
Recall, the definition of the Laplace transform. According to this, the Laplace of f(t) is given by the integral
L{f(t)} = $\int_0^\infty$ e-st f(t) dt
Let f(t) = t.
∴ L{t} = $\int_0^\infty$ te-st dt
= $\Big[t\int e^{-st} dt – \int \{\frac{d}{dt}(t) \int e^{-st} dt\} dt \Big]_0^\infty$, using the integration by parts.
= $\Big[ t \cdot \dfrac{e^{-st}}{-s} – \int \dfrac{e^{-st}}{-s} dt \Big]_0^\infty$
= $\Big[ \dfrac{te^{-st}}{-s} – \dfrac{e^{-st}}{s^2} \Big]_0^\infty$
= $\lim\limits_{t \to \infty}\Big( \dfrac{te^{-st}}{-s} – \dfrac{e^{-st}}{s^2} \Big)$ $-\big( 0- \dfrac{1}{s^2}\big)$
= $0-0 + \dfrac{1}{s^2}$ as limt→∞ e-st=0.
= $\dfrac{1}{s^2}$.
So the Laplace transform of t is 1/s2.
| L{t} = 1/s2. |
Related Topics:
FAQs
Q1: What is the Laplace transform of t?
Answer: The Laplace transform of t is equal to 1/s2.
Q2: Find L{t}.
Answer: L{t} = 1/s2.