Limit of sin(√x)/x as x approaches 0

The limit of sin(√x)/x as x approaches 0 DOES NOT exist, that is, the lim_x→0 sin(\sqrt{x})/x formula is given by

$\lim\limits_{x \to 0} \dfrac{\sin \sqrt{x}}{x}=$ not exist.

Let us learn how to find the limit of sin root x divided by x when x tends to 0.

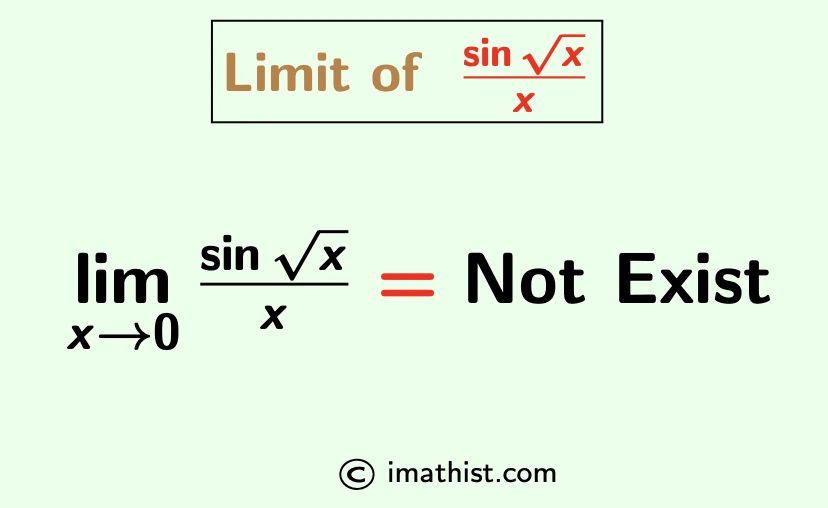
Find Limit of sin(√x)/x when x→0

We have

$\lim\limits_{x \to 0} \dfrac{\sin \sqrt{x}}{x}$

= $\lim\limits_{x \to 0} \dfrac{\sin \sqrt{x}}{\sqrt{x}} \times \dfrac{1}{\sqrt{x}}$

= $\lim\limits_{x \to 0} \dfrac{\sin \sqrt{x}}{\sqrt{x}} \times \lim\limits_{x \to 0} \dfrac{1}{\sqrt{x}}$ by the product rule of limits.

[Let √x=z, so that z→0 as x→0]

= $\lim\limits_{z \to 0} \dfrac{\sin z}{z} \times \lim\limits_{x \to 0} \dfrac{1}{\sqrt{x}}$

= 1 × 1/0 using the formula lim_x→0 sinx/x =1.

= does not exist.

So the limit of sin(√x)/x does not exist as x→0.

More reading:

Limx→0 x/sinx	Limx→∞ sinx/x
Limx→0 sin(1/x)	Limx→0 sin3x/sin2x
Limx→0 tanx/x	Limx→0 (cosx-1)/x

Limit of sin(√x)/2x as x→0

The given limit can be written as follows:

$\lim\limits_{x \to 0} \dfrac{\sin \sqrt{x}}{2x}$ = $\dfrac{1}{2} \lim\limits_{x \to 0} \dfrac{\sin \sqrt{x}}{x}$

So by the above limit we prove, we conclude that the limit of sin(√x)/2x as x→0 does not exist.

More Limits:

Limx→0 sin(x2)/x	Limx→0 (ax-1)/x
Limx→0(ex-1)/x	Limx→0 log(1+x)/x

FAQs