The cot2x identity is given by cot2x = (cot2x-1)/2cotx. Note that cot2x is the cotangent of the angle 2x. The cot2x formula is as follows:
cot2x = $\dfrac{\cot^2 x -1}{2 \cot x}$.
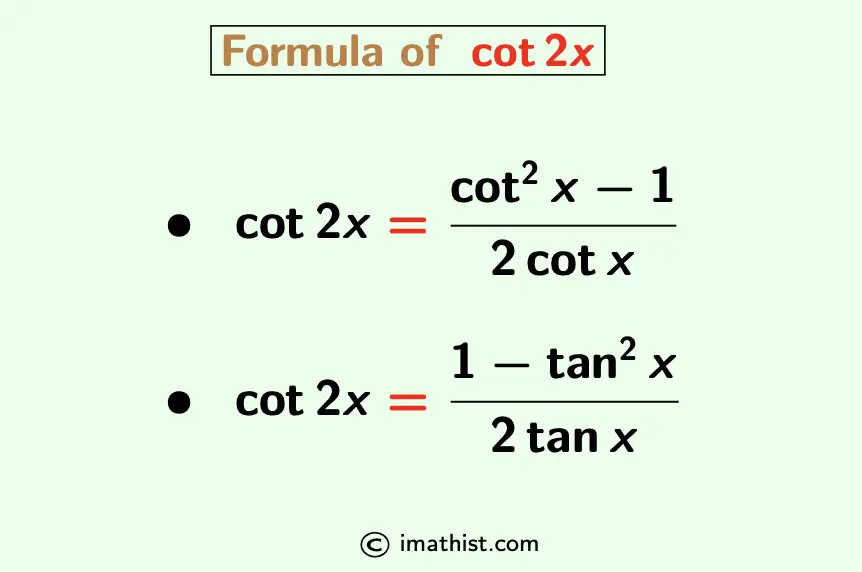
Let us now learn how to prove the cot2x identity.
Cot2x Formula in Terms of cotx
The cot2x formula in terms of cotx is given as follows.
$\boxed{\cot 2x = \dfrac{\cot^2 x -1}{2 \cot x}}$.
Proof:
cot2x = cot(x+x)
= $\dfrac{\cot x \cot x -1}{\cot x +\cot x}$ using the formula cot(a+b) = (cot a cot b -1)/(cot a + cot b)
= $\dfrac{\cot^2 x -1}{2\cot x}$.
So the cot2x formula in terms of cotx is equal to cot2x = (cot2x-1)/2cotx.
You Can Read: Sec2x Identity, Formula | Cosec2x Identity, Formula
Cot2x Formula in Terms of tanx
The cot2x formula in terms of tanx is given below.
$\boxed{\cot 2x = \dfrac{1-\tan^2 x}{2 \tan x}}$.
Proof:
From the above, we have that
$\cot 2x = \dfrac{\cot^2 x -1}{2 \cot x}$
As cotx=1/tanx, we deduce that
$\cot 2x = \dfrac{\frac{1}{\tan^2 x} -1}{\frac{2}{\tan x}}$
$\Rightarrow \cot 2x = \dfrac{1-\tan^2 x}{2\tan x}$.
So the cot2x formula in terms of tanx is equal to cot2x = (1 – tan2x)/2tanx.
Read Also: Sin3x Formula, Identity | Sin3x Formula
Remark:
Note that
- cot2x = $\dfrac{1}{\tan 2x}$
- cot2x in terms of tanx and cotx is given by cot2x = $\dfrac{1}{2}(\cot x -\tan x)$
FAQs
Q1: What is the formula of cot2x in terms of tanx?
Answer: The cot2x formula in terms of tanx is given by cot2x = (1 – tan2x)/2tanx.
Q2: What is the formula of cot2x in terms of cotx?
Answer: The cot2x formula in terms of cot2x is given by cot2x = (cot2x-1)/2cotx.