Integral of natural log of x: Formula, Proof

The natural log of x is the logarithm of x with base e, and it is denoted by ln(x). That is, log_ex = lnx. The integral of natural log of x is equal to ∫ln(x) dx = xln(x) -x+C, where C is a constant. Here, we will learn how to find the integration of natural log of x.

The formula of the integration of natural log of x is given as follows:

∫ln(x) dx = = xln(x) -x+C.

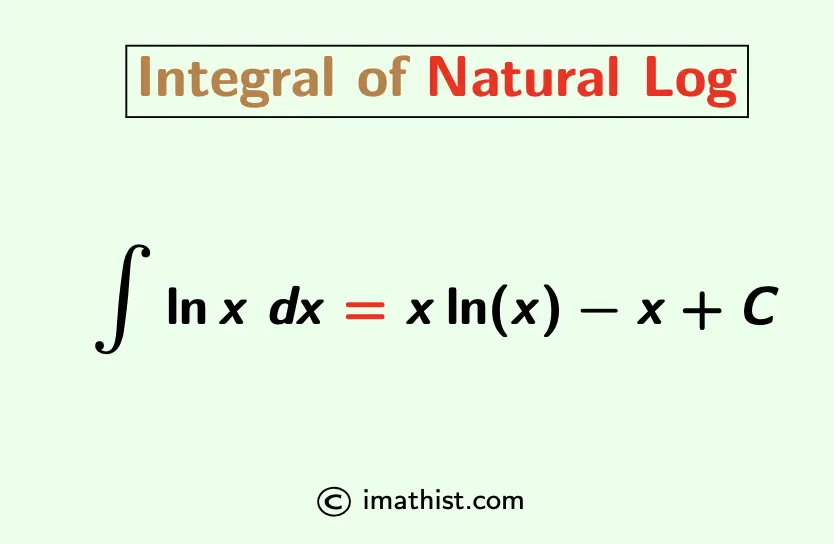
Find Integral of Natural log of x

Question: Find ∫ln(x) dx.

Solution:

To integrate natural log of x, we use integration by parts formula:

∫uv dx = u ∫v dx – ∫[$\frac{du}{dx}$∫v dx] dx.

Let us put u=ln(x) and v=1. Therefore,

∫ln(x) dx = ∫ ln(x) ⋅ 1 dx

= ln(x) ∫1 dx – ∫ $\big[\dfrac{d}{dx}(\ln x) \int 1\ dx \big]dx$

= $\ln x \times x -\int \big[\dfrac{1}{x} \times x \big]dx$ + C

= x ln(x) – ∫dx + C

= x ln(x) – x + C.

So the integral of natural log of x using integration by parts is given by ∫ln(x) dx = x ln(x) – x + C where C denotes an arbitrary constant.

Read Also: Integration of root tanx

Integration of root tanx + root cotx

FAQs