Integral of ln2x | How to Integrate of ln2x

The integral of ln2x is equal to x(ln2x−1)+C where C is a constant. Here, we will learn how to integrate ln2x.

The integration of ln(2x) is given as follows:

∫ln2x dx = x(ln2x−1)+C

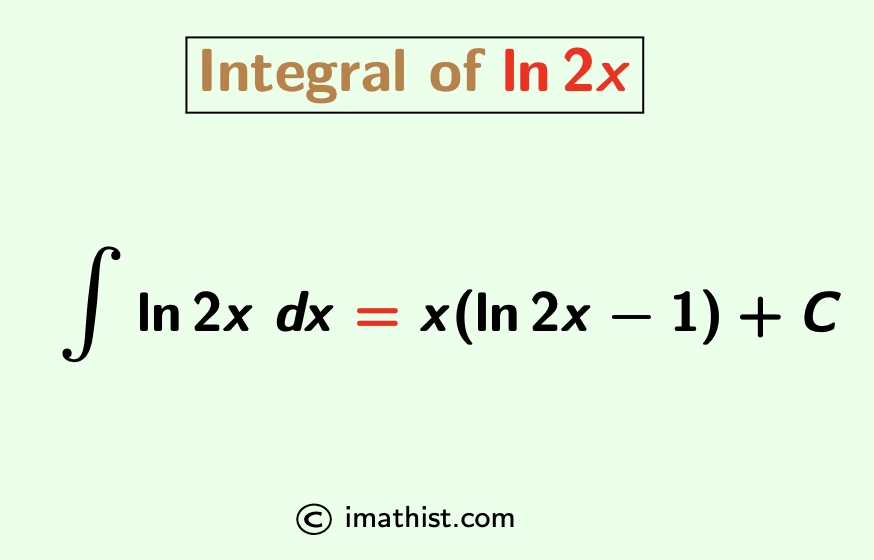
Integration of ln2x

Question: What is the integration of ln2x?

Solution:

To find the integration of ln2x, we will use the integration by parts formula. This formula is used to find the integral of the product uv, where u and v are two functions of x.

Integration by parts formula: ∫uv dx = u ∫v dx – ∫[$\frac{du}{dx}$∫v dx] dx.

Put u=ln2x and v=1.

Therefore,

∫ln(2x) dx = ∫ (ln2x ⋅ 1) dx

= ln2x ∫1 dx – ∫ $\big[\dfrac{d}{dx}(\ln 2x) \int 1\ dx \big]dx$

= $\ln 2x \times x -\int \big[\dfrac{1}{x} \times x \big]dx$ + C, as the derivative of ln2x is 1/x.

= x ln2x – ∫dx + C

= x ln2x – x + C

= x (ln2x – 1) + C.

So the integral of ln2x using integration by parts is equal to ∫ln2x dx = x(ln2x – 1) +C where C denotes an arbitrary integration constant.

More Integrals:

Integral of ln(x)

How to integrate sin³x

Integration of natural log of x

Integration of $\frac{x}{1+x^2}$

FAQs