The limit of (1+1/x)^x as x approaches infinity is equal to e. Here we will discuss Lim x→∞ (1+(1/x))^x formula with proof.
Note that
Limx → ∞ (1+$\frac{1}{x}$)x = e.
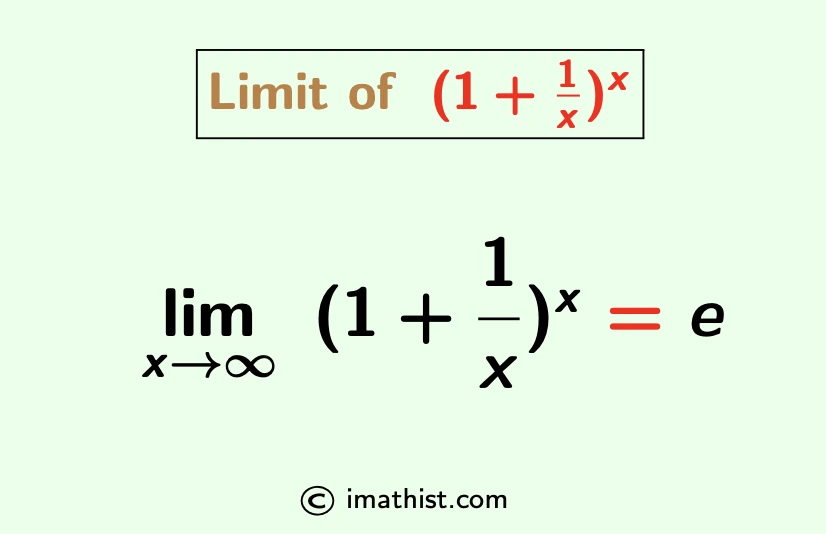
Limx→∞ (1+(1/x))x Formula with Proof
The formula of limx→∞ (1+(1/x))x is given by limx → ∞ (1+(1/x))x =e.
Explanation:
Let y = limx→∞ (1+$\frac{1}{x}$)x.
So we need to find y.
Taking natural logarithm ln on both sides, we get that
ln y = ln limx→∞ (1+$\frac{1}{x}$)x
⇒ ln y = limx→∞ ln (1+$\frac{1}{x}$)x
⇒ ln y = limx→∞ x ln(1+$\frac{1}{x}$) as we know ln limx→∞ f(x) = limx→∞ ln f(x).
Take 1/x = z.
Then z→0 as x→∞. So from above we get that
ln y = limz→0 $\dfrac{\ln (1+z)}{z}$
⇒ ln y = 1 using the formula limx→0 $\dfrac{\ln (1+x)}{x}$ =1.
⇒ ln y = ln e
⇒ y = e.
In other words, limx→∞ (1+$\frac{1}{x}$)x =e.
So the limit of (1+1/x)x as x approaches Infinity is equal to e.
Read Also: Limit of cosx/x when x→∞
FAQs
Q1: What is the limit of (1+1/x)x when x tends to infinity?
Answer: The limit of (1+1/x)x when x tends to infinity is equal to e, that is, limx → ∞ (1+1/x)x = e.
Q2: What is Limx → ∞ (1+(1/x))x?
Answer: Limx → ∞ (1+(1/x))x = e.