The limit of x^1/x as x approaches infinity is equal to 1. This limit is denoted by limx→∞ x1/x, so the formula for the limit of x1/x when x tends to infinity is given by
limx→∞ x1/x = 1.
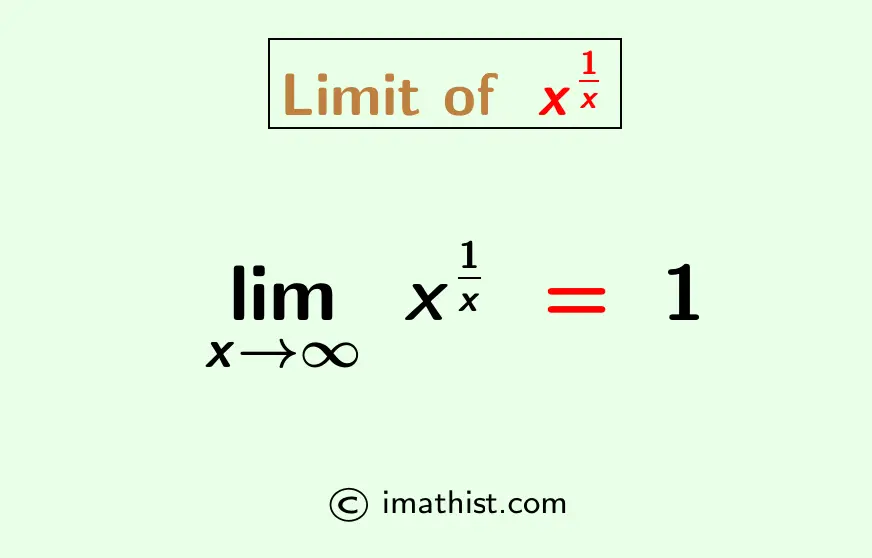
Let us now find the limit of x to the power 1/x when x tends to ∞.
Proof of Limit x1/x when x→∞
| Answer: The limit of x1/x when x→∞ is equal to 1. |
Explanation:
Step 1:
Use the exponential formula: $x^y=e^{\ln(x^y)}$. Thus, the given limit will be
limx→∞ x1/x = limx→∞ $e^{\ln(x^{1/x})}$
⇒ limx→∞ x1/x = limx→∞ $e^{\frac{1}{x} \ln(x)}$ using the formula ln(xy) = y ln(x).
⇒ limx→∞ x1/x = $e^{\lim\limits_{x \to \infty} \frac{\ln x}{x}}$ …(∗)
Step 2:
Now we compute the limit limx→∞ $\dfrac{\ln x}{x}$.
Note that this has the indeterminate form ∞/∞. So using the l’Hospital’s Rule, we obtain that
limx→∞ $\dfrac{\ln x}{x}$ = limx→∞ $\dfrac{1/x}{1}$ = limx→∞ $\dfrac{1}{x}$ = 0.
Step 3:
Using limx→∞ ln(x)/x = 0, we deduce from (∗) that
limx→∞ x1/x = e0 = 1.
So the limit of x1/x is equal to 1 when x approaches 0.
More Limits:
limx→0 (cosx -1)/x | limx→0 cosx/x
FAQs
Q1: What is the limit of x1/x when x tends to infinity?
Answer: The limit of x1/x when x tends to infinity is equal to 1, that is, limx→∞ x1/x = 1.