The limit of x sin(1/x) as x approaches 0 is equal to 0. This limit is denoted by limx→0 xsin(1/x). So the formula for the limit of x sin(1/x) when x tends to zero is as follows.
limx→0 x sin(1/x) = 0.
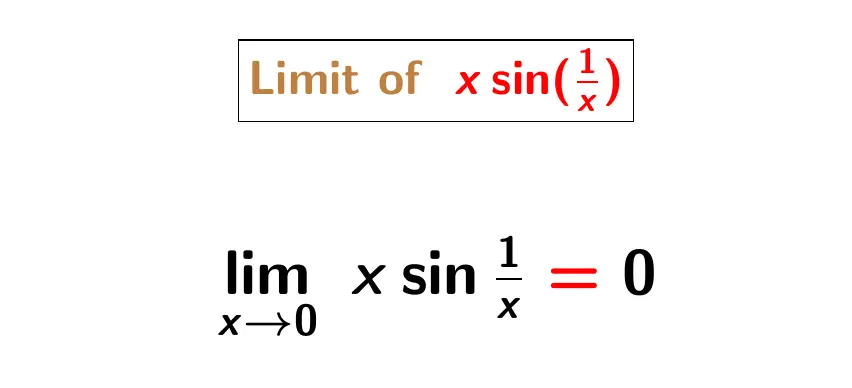
Let us now find the limit of xsin(1/x) using the Squeeze/Sandwich theorem.
Proof of Limx→0 xsin(1/x) =0 by Squeeze Theorem
| Answer: The limit limx→0 xsin(1/x) is equal to 0. |
Explanation:
Step 1:
From the Trigonometry we know that sinθ lies between -1 and 1 for any real values of θ. Thus we have that
-1 ≤ sin(1/x) ≤ 1.
Taking modulus, we get that
0 ≤ |sin(1/x)| ≤ 1.
Step 2:
Multiplying both sides by |x|, it follows that
0 ≤ |x| |sin(1/x)| ≤ |x|
⇒ 0 ≤ |xsin(1/x)| ≤ |x|.
Step 3:
Taking limx→0 on both sides, we get
limx→0 (0) ≤ limx→0 |x sin(1/x)| ≤ limx→0 |x|.
⇒ 0 ≤ limx→0 |x sin(1/x)| ≤ 0.
Thus, by the Squeeze theorem, limx→0 |x sin(1/x)| = 0.
As we know that limx→0|f(x)| = 0 ⇒ limx→0 f(x) = 0, it follows that limx→0 xsin(1/x) = 0.
Conclusion: So the limit of xsin(1/x) is equal to 0 when x tends to 0, and this is obtained by the Squeeze theorem. That is,
| limx→0 xsin(1/x) = 0 |
More Limits:
FAQs
Q1: What is the limit of xsin(1/x) as x approaches 0?
Answer: The limit of xsin(1/x) as x approaches 0 is equal to 1, that is, limx→0 x sin(1/x) =0.