The formula of 1-cos2x is given by 1-cos2x=2sin2x. In this post, we establish 1-cos2x formula and identity with some solved examples.
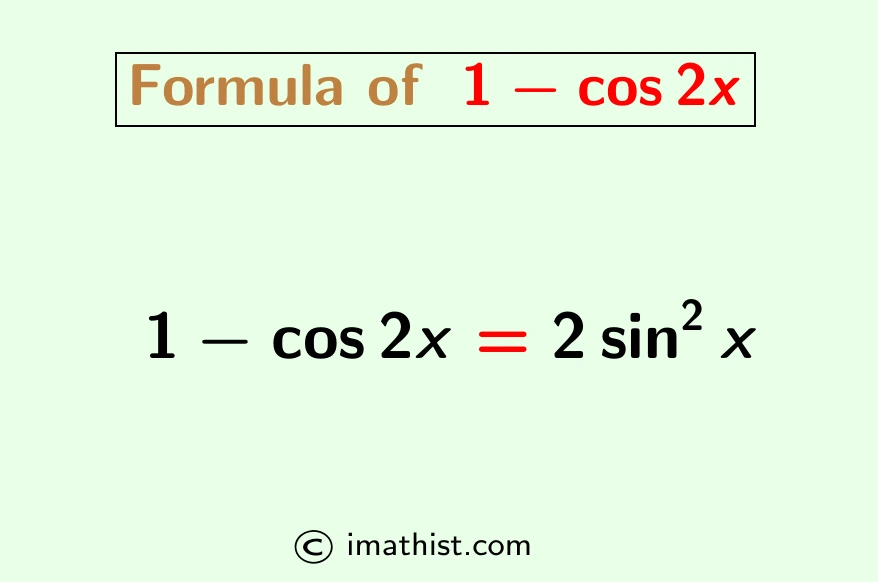
Formula of 1-cos2x
Answer: The 1-cos2x formula is 1-cos2x=2sin2x.
Proof:
Using the formula cos2θ= cos2θ -sin2θ, the given expression can be written as follows.
1-cos2x
= 1- (cos2x -sin2x)
= (1- cos2x) -sin2x
= sin2x -sin2x
= 2sin2x.
Thus, 1-cos2x = 2sin2x.
So the formula of 1-cos2x is given as follows:
$\boxed{1-\cos 2x = 2\sin^2 x}$
Therefore, the simplification of 1-cos2x is 1-cos2x = 2sin2x.
Also Read:
Question-Answer
Question1: Find the value of 1-cos120°.
Answer:
Using the above formula 1 – cos2x = 2sin2x, we have
1-cos120° = 2sin260° = 2 × (1/2)2 = 2/4 = 1/2.
Thus, the value of 1-cos120° is 1/2.
FAQs
Q1: What is the identity of 1-cos2x?
Answer: The identity of 1-cos2x is equal to 1-cos2x = 2sin2x.
Q2: What is the formula of 1-cos2θ?
Answer: The formula of 1-cos2θ is equal to 1-cos2θ = 2sin2θ.