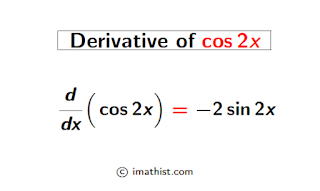Derivative of cos2x by First Principle, Chain Rule

The derivative of cos2x is equal to -2sin2x.  In this post, we will find the derivative of cos2x by the first principle, that is, by the limit definition of derivatives as well as by the chain rule of derivatives.

Recall the first principle of derivatives. By this rule, we know that the derivative of a function f(x) is given by the following limit:

${\displaystyle \frac{d}{dx}}(f(x))$$=\underset{h\to 0}{lim}{\displaystyle \frac{f(x+h)-f(x)}{h}}$ …(I)

Derivative of cos2x by First Principle

Question: What is the derivative of cos 2x?

Answer: The derivative of cos2x is -2sin2x.

Explanation:

Step 1: We put $f(x)=\cos 2x$ in the above formula (I). Step 2: Thus the derivative of cos2x by the first principle will be equal to

${\displaystyle \frac{d}{dx}}(\cos 2x)$$=\underset{h\to 0}{lim}{\displaystyle \frac{\cos 2(x+h)-\cos 2x}{h}}$

Step 3: Now apply the formula $\cos a-\cos b$ $=-2\sin {\displaystyle \frac{a+b}{2}}\sin {\displaystyle \frac{b-a}{2}}$. By doing so we obtain that

${\displaystyle \frac{d}{dx}}(\cos 2x)$$=\underset{h\to 0}{lim}{\displaystyle \frac{-2\sin (2x+h)\sin h}{h}}$

= $-2\underset{h\to 0}{lim}\sin (2x+h)$ $\cdot \underset{h\to 0}{lim}{\displaystyle \frac{\sin h}{h}}$

= $-2\sin (2x+0)$ $\times 1$ as we know that limit of sinh/h is 1 when h tends to zero.

= $-2\sin 2x$.

Conclusion: Therefore, the derivative of cos2x is 2sin2x, obtained by the first principle of derivatives, that is, d/dx(cos2x) = −2sin2x.

Also Read:

Derivative of cos(ex)	Derivative of log(3x)
Derivative of sin5 x	Derivative of (sinx)logx

Question-Answer on Derivative of cos2x

Question: What is the derivative of cos2x at x=0.

Answer: From the above, we have obtained that the derivative of cos2x is -2sin2x. So the derivative of cos2x at x=0 is equal to

$[{\displaystyle \frac{d}{dx}}(\cos 2x)]x=0$ $=[-2\sin 2x]x=0$

$=-2\sin 0$

$=-2\times 0$ as the value of sin0 is 0.

$=0$.

Thus, the derivative of cos2x at x=0 is equal to 0.

More Reading: Derivative of root(x) + 1/root(x)

Derivative of cos2x by Chain Rule

We now find the derivative of cos2x by the chain rule. Let us put $z=2x$. Thus, ${\displaystyle \frac{dz}{dx}}=2$. Then by the chain rule, the derivative of cos2x is given by

${\displaystyle \frac{d}{dx}}(\cos 2x)={\displaystyle \frac{d}{dz}}(\cos z)\cdot {\displaystyle \frac{dz}{dx}}$

= $-\sin z\cdot 2$

=$-2\sin 2x$ as z=2x.

So the derivative of cos2x by the chain rule is equal to -2sin2x.

RELATED TOPICS:

Derivative of x^3/2 | Derivative of 1/xⁿ

Derivative of e^1/x

Derivative of 1/sinx | Derivative of ln(ln x)

FAQs