Derivative of 1/2x (1 by 2x)

The derivative of 1/2x is equal to -1/2x². In this post, we will learn how to find the derivative of 1 divided by 2x. The derivative formula of 1/2x is given by

$\dfrac{d}{dx}(\dfrac{1}{2x})= – \dfrac{1}{2x^2}$.

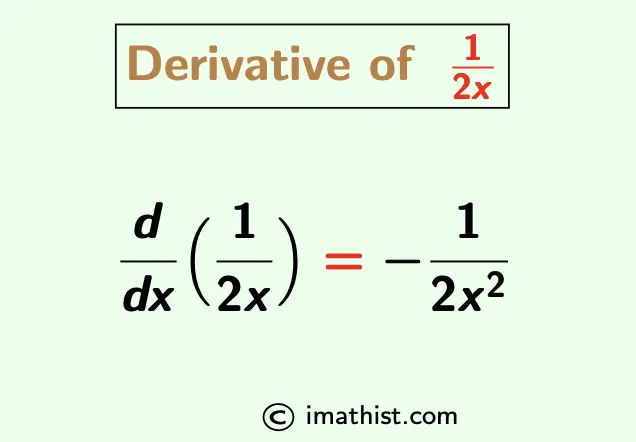
Derivative of 1/2x by Power Rule

Let us find the derivative of 1 by 2x by the power rule of derivatives. We have:

$\dfrac{d}{dx}(\dfrac{1}{2x})$

= $\dfrac{1}{2} \dfrac{d}{dx}(\dfrac{1}{x})$

= $\dfrac{1}{2} \dfrac{d}{dx}(x^{-1})$

= 1/2 × (-1 ⋅ x^-1-1) by the power rule of derivatives d/dx(xⁿ) = nx^n-1.

= -1/2 × x^-2

= -1/2x²

Hence, the derivative of 1/2x is -1/2x² and this is proved by the power rule of derivatives.

Derivative of 1 by 2x

Let z= $\dfrac{1}{2x}$ We need to find dz/dx.

So 2zx = 1.

Differentiating both sides with respect to x and applying the chain rule of derivatives, we get that

2 (z $\dfrac{dx}{dx}$ + x$\dfrac{dz}{dx}$) = 0 as the derivative of the constant 1 is equal to 0.

⇒ z $\dfrac{dx}{dx}$ + x$\dfrac{dz}{dx}$ = 0

⇒ z ⋅ 1 + x $\dfrac{dz}{dx}$ = 0

⇒ x $\dfrac{dz}{dx}$ = -z

⇒ $\dfrac{dz}{dx}$ = -z/x

∴ dz/dx = -1/2x² as z=1/2x.

So the derivative of 1/2x is equal to -1/2x².

Have You Read These Derivatives?

Derivative of 1/x

Derivative of √x

Derivative of √3x

Derivative of √x -1

FAQs