Derivative of cos root x

The derivative of cos root x is equal to (-sin√x)/2√x. Here we will find the derivative of cos√x by the chain rule of derivatives.

The differentiation of cos(√x) with respect to x is given by

$\dfrac{d}{dx}(\cos \sqrt{x})=-\dfrac{\sin \sqrt{x}}{2\sqrt{x}}$.

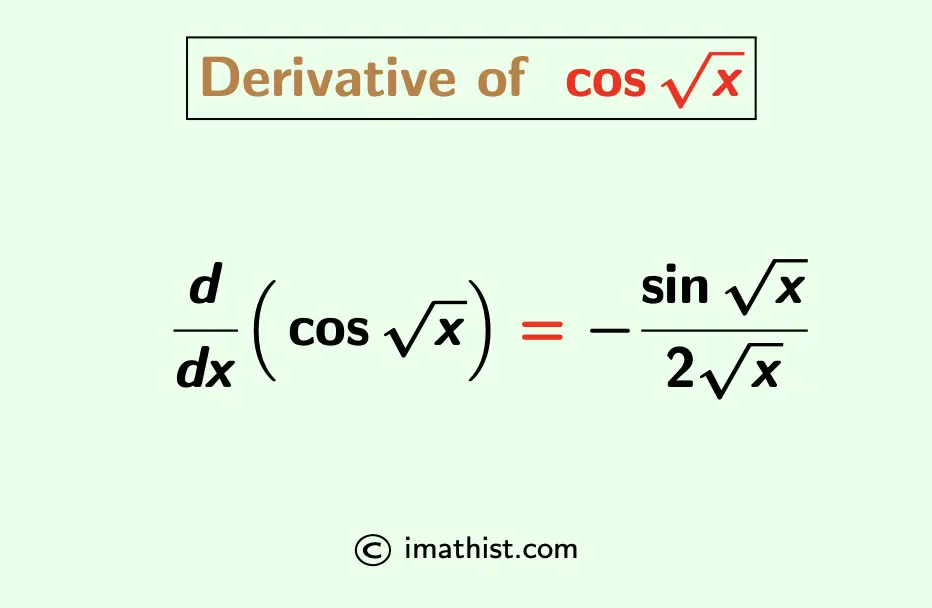
Let us now find the derivative of cos root x using the chain rule of differentiation.

Derivative of cos(√x) by Chain Rule

To find the derivative of cos root x, we will use the chain rule of differentiation. Let us assume that

z = √x.

Differentiating, dz/dx = d/dx(x^1/2) = 1/2 x^1-1/2 = 1/(2√x), by the power rule.

Now,

$\dfrac{d}{dx}(\cos \sqrt{x})$

= $\dfrac{d}{dx}(\cos z)$

= $\dfrac{d}{dz}(\cos z) \times \dfrac{dz}{dx}$, by the chain rule.

= $-\sin z \times \dfrac{1}{2\sqrt{x}}$ as we have dz/dx = 1/(2√x).

= $-\dfrac{\sin \sqrt{x}}{2\sqrt{x}}$ as z=√x.

So the derivative of cos root x is equal to (-sin√x)/2√x, and this is obtained by the chain rule of differentiation.

Read Also

Derivative of sinx/x

Derivative of cos square x

Derivative of $\sqrt{\sec x}$

FAQs