Derivative of Fifth Root of x

The derivative of fifth root of x is 1/(5x^4/5). In this post, we will learn how to find the derivative of the fifth root x. Here, we will use the power rule of derivatives.

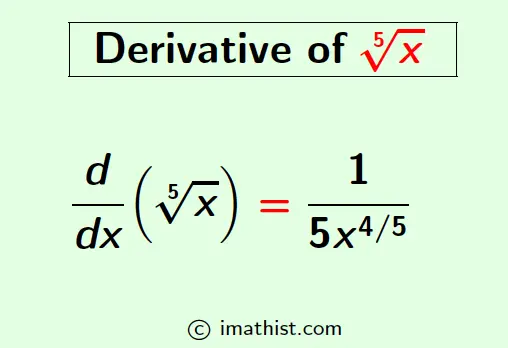
Note that the fifth root of x can be written as

$\sqrt[5]{x}$

Or, following the rule of indices, the fifth root of x is equal to x^1/5.

The derivative formula of fifth root x is given by

$\dfrac{d}{dx}(\sqrt[5]{x})=\dfrac{1}{5x^{4/5}}$.

Derivative of Fifth Root x

By the rule of indices, the fifth root of x can be written as x^1/5. As it is a power of x, we can use the power rule of derivatives which says that the derivative of xⁿ (for an integer n) is equal to

$\dfrac{d}{dx}$(xⁿ)=nx^n-1.

Thus the derivative of the fifth root of x will be equal to

$\dfrac{d}{dx}(\sqrt[5]{x})$

= $\dfrac{d}{dx}$(x^1/5)

= $\dfrac{1}{5} x^{\frac{1}{5}-1}$ by the above power rule.

= $\dfrac{1}{5} x^{\frac{-4}{5}}$

= 1/(5x^4/5).

So the derivative of the fifth root of x is 1/(5x^4/5) and this is proved by the power rule of derivatives.

Question 1: What is the derivative of the fifth root of x at x=1?

Solution:

From above we obtain that the derivative of the fifth root of x is 1/(5x^4/5). So the derivative of fifth root x at the point x=1 is equal to

$\dfrac{d}{dx}(x^{\frac{1}{5}})|_{x=1}$

= $[\dfrac{1}{5x^{4/5}}]_{x=1}$

= $\dfrac{1}{5\cdot 1^{4/5}}$

= 1/5.

So the derivative of fifth root of x at x=1 is equal to 1/5.

Question 2: What is the derivative of 5?

Solution:

Note that f(x)=5 is a constant function of x. As the Derivative of a constant is 0, the derivative of 5 is 0.

Using the above logic, the derivative of root 5 is equal to 0.

Derivative of Fifth Root of 1

The fifth roots of 1 are the solutions of the equation x⁵=1. As these solutions are constants, using the Derivative of a constant is zero property, we can obtain that the derivative of the fifth root of 1 is zero.

Also Read:

Derivative of 1/lnx

Derivative of square root 2x

Derivative of root 3x

Derivative of Fourth Root of x

FAQs