Find Derivative of ln3x | Ln3x Differentiation

The derivative of ln3x is equal to 1/x, where ln denotes the natural logarithm. Here we will find the derivative of ln(3x).

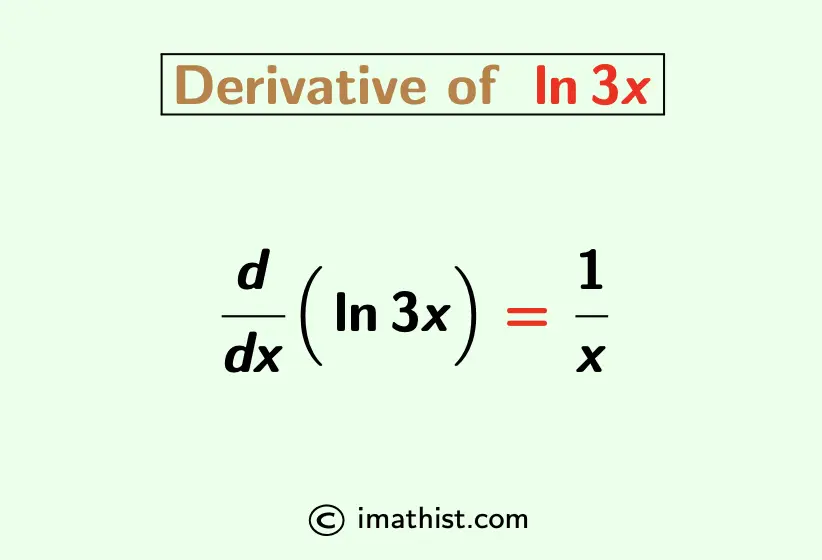
The ln3x differentiation formula is given below:

$\dfrac{d}{dx}(\ln 3x)=\dfrac{1}{x}$.

ln(3x) Derivative

Question: Find the derivative of ln3x.

Solution:

By the logarithm rule for products,

ln 3x = ln3 + lnx.

So, $\dfrac{d}{dx}(\ln 3x)$ = $\dfrac{d}{dx}(\ln 3) + \dfrac{d}{dx}(\ln x)$, by the sum rule of differentiation.

= $0 +\dfrac{1}{x}$, as the derivative of a constant is 0 and ln3 is a constant. Also, the derivative of lnx is 1/x.

= $\dfrac{1}{x}$.

So the derivative of ln3x is equal to 1/x.

You can read: Derivative of 1/x

What is the derivative of 1/lnx?

Derivative of ln3x by Chain Rule.

Let z=3x.

So dz/dx=3.

Now, by the chain rule,

$\dfrac{d}{dx}(\ln 3x)$ = $\dfrac{d}{dz}(\ln z) \times \dfrac{dz}{dx}$

= $\dfrac{1}{z} \times 3$

= $\dfrac{3}{3x}$

= 1/x.

Therefore, the derivative of ln3x is equal to 1/x, and it is obtained by the chain rule of differentiation.

More Reading: How to find the derivative of 1/sinx?

FAQs