The derivative of lnx^2 is equal to 2/x. The natural logarithm of x2 is denoted by ln(x2), and its derivative formula is given by
$\dfrac{d}{dx}(\ln x^2)=\dfrac{2}{x}.$
That is, the differentiation of ln(x2) is 2/x.
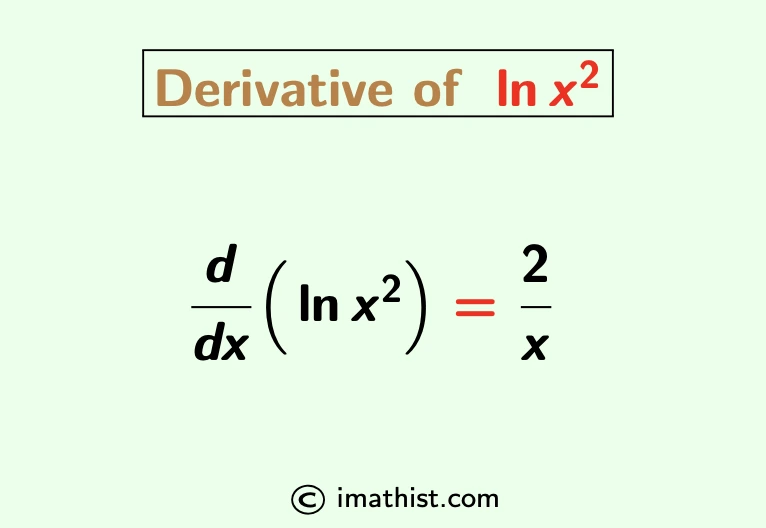
Derivative of ln(x2) by Chain Rule
| Answer: The derivative of ln(x2) is 2/x. |
Explanation:
To find the derivative of ln(x2) by the chain rule, let us put
z = x2.
So $\dfrac{dz}{dx}$ = 2x.
Now,
$\dfrac{d}{dx}(\ln x^2)$ = $\dfrac{d}{dz}(\ln z) \times \dfrac{dz}{dx}$
= $\dfrac{1}{z} \times 2x$
= $\dfrac{2x}{z}$
= $\dfrac{2x}{x^2}$ as z=x2.
= $\dfrac{2}{x}$.
So the derivative of ln(x2) is equal to 2/x, and this is obtained by the chain rule of differentiation.
More Derivatives:
FAQs
Q1: What is the derivative of ln(x2)?
Answer: The derivative of ln(x2) with respect to x is equal to 2/x.
Q2: If y=ln(x2), then find dy/dx.
Answer: If y= ln(x2), then dy/dx =2/x.