Derivative of tan root x: Formula, Proof by Chain Rule

The derivative of tan root x is equal to (sec²√x)/2√x. By the chain rule of differentiation, the derivative formula of tan(√x) with respect to x is given as follows:

$\dfrac{d}{dx}(\tan \sqrt{x})=\dfrac{\sec^2 \sqrt{x}}{2\sqrt{x}}$.

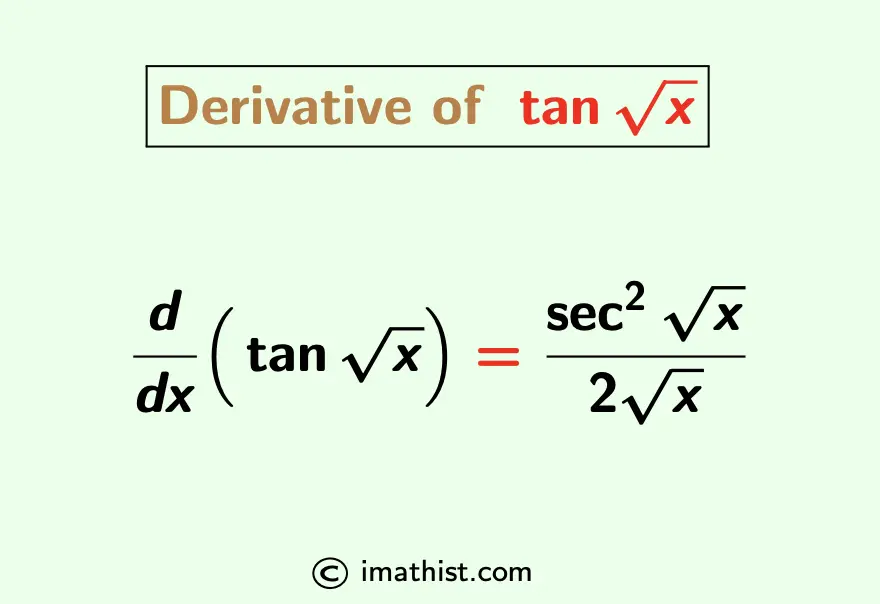
Derivative of tan(√x) by Chain Rule

Answer: The derivative of tan√x is (sec²√x)/2√x.

Explanation:

Let us put

z = √x.

Differentiating both sides w.r.t. x, we get that

dz/dx = d/dx(x^1/2) = 1/2 x^1-1/2 = 1/(2√x) [by the power rule of differentiation].

Now, the given derivative

$\dfrac{d}{dx}(\tan \sqrt{x})$

= $\dfrac{d}{dx}(\tan z)$

= $\dfrac{d}{dz}(\tan z) \times \dfrac{dz}{dx}$, by the chain rule of differentiation.

= $\sec^2 z \times \dfrac{1}{2\sqrt{x}}$ as we have dz/dx = 1/(2√x).

= $\dfrac{\sec^2 \sqrt{x}}{2\sqrt{x}}$, putting back the value of z=√x.

So the derivative of tan root x is equal to (sec²√x)/2√x, and this is proved by the chain rule of differentiation.

Also Read

Derivative of cos root x

Derivative of cos square x

Derivative of $\sqrt{\tan x}$

FAQs