Derivative of x^cosx | x^cosx Derivative

The derivative of x^cosx (x to the power cosx) is equal to x^cosx[cosx/x – sinx log_ex]. Here we learn how to differentiate x^cosx.

The derivative of x^cosx is denoted by d/dx(x^cosx) and its formula is given below:

d/dx(x^cosx) = x^cosx[cosx/x – sinx log_ex].

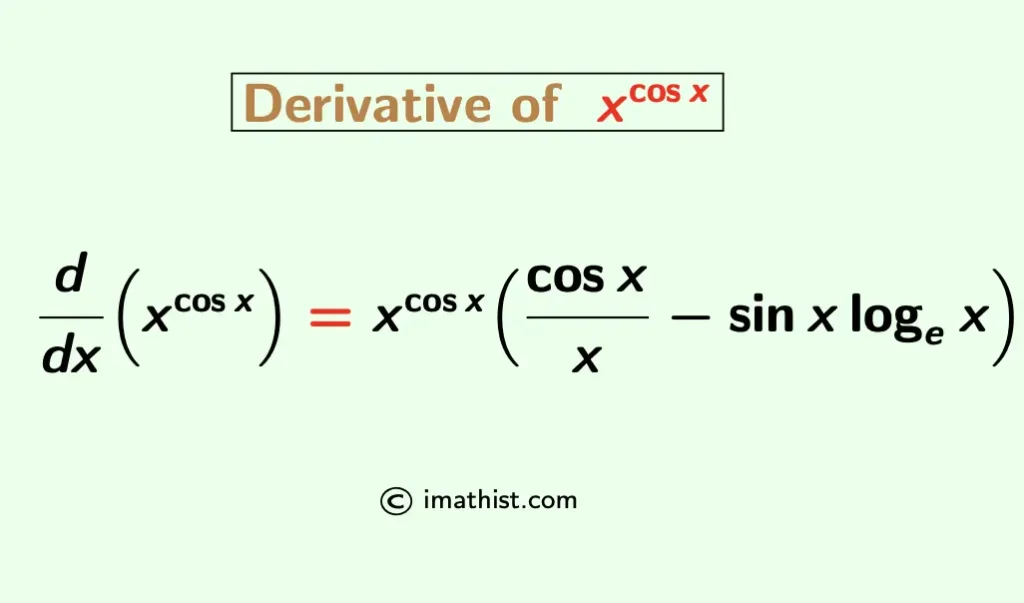
Let us now give a proof of x^cosx derivative.

Differentiate x^cosx

Question: Prove that d/dx(x^cosx) = x^cosx[cosx/x – sinx logx].

Answer:

To differentiate x^cosx, we will use the logarithmic differentiation. Let us put

y=x^cosx.

So we need to find dy/dx. Taking the natural logarithms both sides, we get that

log_e y = log_e x^cosx

⇒ log_ey = cosx log_ex, using the logarithm formula: log_abⁿ = n log_ab.

Differentiating both sides w.r.t x, we have

$\dfrac{d}{dx}(\log_e y)=\dfrac{d}{dx}(\cos x \log_e x)$

⇒ $\dfrac{1}{y} \dfrac{dy}{dx}$ $=\cos x\dfrac{d}{dx}(\log_e x)+\log_e x\dfrac{d}{dx}(\cos x)$, by the product rule of derivatives.

⇒ $\dfrac{1}{y} \dfrac{dy}{dx}$ $=\cos x \cdot \dfrac{1}{x}+\log_e x (-\sin x)$ as the derivative of log_ex is 1/x and d/dx(cos x)= -sinx.

⇒ $\dfrac{dy}{dx}=y(\dfrac{\cos x}{x}-\sin x\log_e x)$

⇒ $\dfrac{dy}{dx}=x^{\cos x}(\dfrac{\cos x}{x}-\sin x \log_e x)$ as y=x^cosx.

So the derivative of x^cosx (x to the cosx) is equal to x^cosx[cosx/x – sinx logx], and it is obtained by the logarithmic differentiation.

More Derivatives:

Derivative of x^x | Derivative of x^sinx

Derivative of x sinx

Derivative of x^3/2

Derivative of sinx/x | Derivative of x^logx

FAQs