What is the Derivative of x^logx

The derivative of x^logx (x to the power logx) is equal to 2 logx x^logx-1. Here we find the differentiation of x^logx by using the product rule of derivatives together with logarithmic differentiation.

The product rule of derivatives states the following:

$\dfrac{d}{dx}$(f(x)g(x)) = f(x) $\dfrac{d}{dx}$(g(x)) + g(x) $\dfrac{d}{dx}$(f(x)) …(I)

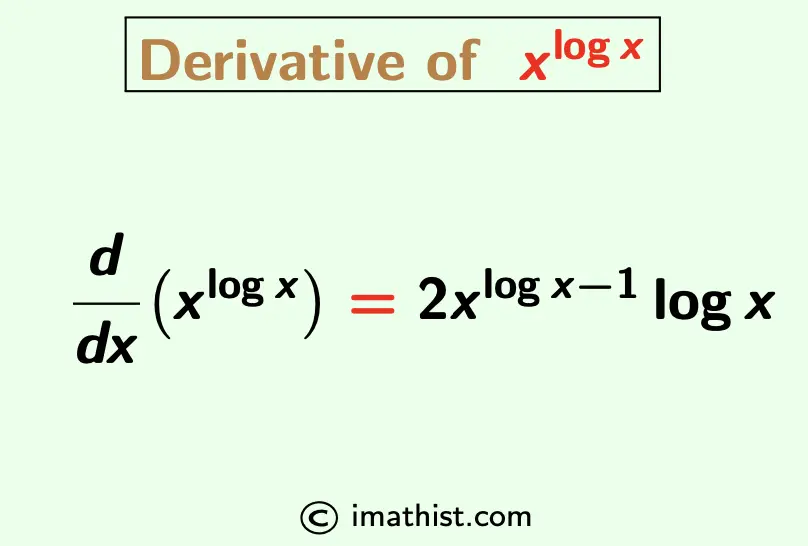
Find the Derivative of x^logx

Answer: The derivative of xlog x is 2xlogx-1 logx.

We find the derivative of x^logx as described below. Here we have considered natural logarithms, that is, logx = log_e x.

Put y=x^logx …(II)

To find $\frac{dy}{dx}$, we use the method of logarithmic differentiation. Taking logarithms on both sides of (II) we get that

log_e y = log_e x^logx

⇒ log y = logx log x, here we have used the logarithm rule: log a^m = m log a.

Differentiating both sides we obtain that

$\dfrac{1}{y}  \dfrac{dy}{dx}=\dfrac{d}{dx}$(logx logx)

⇒ $\dfrac{1}{y}  \dfrac{dy}{dx}$ = logx $\dfrac{d}{dx}$(logx) + logx $\dfrac{d}{dx}$(logx) using the above product rule (I) of derivatives.

⇒ $\dfrac{1}{y}  \dfrac{dy}{dx}$ = logx ⋅ $\dfrac{1}{x}$ + logx ⋅ $\dfrac{1}{x}$

⇒ $\dfrac{dy}{dx}$ = y [$\dfrac{2 \log x}{x}$]

⇒ $\dfrac{dy}{dx}$ = x^logx [$\dfrac{2 \log x}{x}$] as y=x^logx.

⇒ $\dfrac{dy}{dx}$ = 2 logx x^logx-1

So the derivative of x^logx is equal to 2 logx x^logx-1.

Related Derivatives:

Derivative of (sinx)logx	Derivative of xx
Derivative of sinx/x	Derivative of xsinx

FAQs