Find derivative of 1/cosx [Quotient Rule]

The derivative of 1/cos is equal to secx tanx. In this post, we will learn how to differentiate 1 over cosx with respect to x.

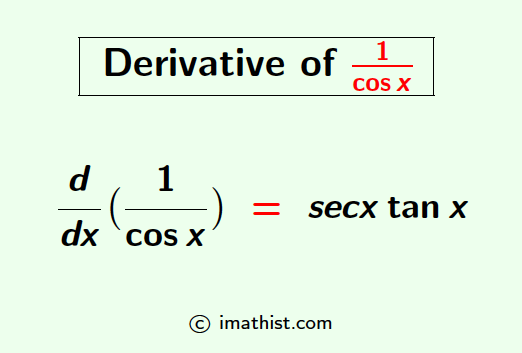
What is the Derivative of 1/cosx?

Answer: The derivative of 1/cosx with respect to x is denoted by d/dx(1/cosx) and it is given below.

$\dfrac{d}{dx}(\dfrac{1}{\cos x})$ = $\sec x \tan x$.

Proof:

As 1/cosx is a quotient function, the best way to find the derivative of 1/cosx is to apply the quotient rule of derivatives. The quotient rule says that

$\dfrac{d}{dx} \left(\dfrac{f}{g} \right)$ = $\dfrac{g \frac{df}{dx} – f \frac{dg}{dx}}{g^2}$

Put f=1 and g=cosx.

So $\dfrac{d}{dx}(\dfrac{1}{\cos x})$

= $\dfrac{\cos x \frac{d}{dx}(1) – 1 \frac{d}{dx}(\cos x)}{\cos^2 x}$

= $\dfrac{\cos x \cdot 0 – 1 \cdot (-\sin x)}{\sin^2 x}$ as the derivative of a constant is zero and the derivative of cosx is -sinx.

= $-\dfrac{\sin x}{\cos^2 x}$

= $- \dfrac{1}{\cos x} \cdot \dfrac{\sin x}{\cos x}$

= $\sec x \tan x$.

Thus the derivative of 1/cosx is sec(x)tan(x) and this is obtained by applying the quotient rule of derivatives.

Remark:

We know that

• The reciprocal of cosx is secx, that is, 1/cosx = secx.
• The derivative of secx is secx tanx.

Using the above two facts, we easily get the derivative of 1/cosx which is given as follows:

d/dx(1/cosx) = secx tanx.

Question: Find the derivative of 1/cos2x.

Answer:

Put t=2x.

By the chain rule of derivatives, we have

d/dx(1/cos2x) = d/dt(1/sint) ⋅ dt/dx

= sect tant ⋅ 2

= 2sec(2x) tan(2x) as t=2x.

Hence, the derivative of 1/cos2x is equal to 2sec(2x) tan(2x).

What is the Derivative of 1-cosx?

As the derivative of cosx is -sinx, by the difference rule of derivatives we have that

$\dfrac{d}{dx}(1-\cos x)$

= $\dfrac{d}{dx}(1)- \dfrac{d}{dx}(\cos x)$

= 0 – (-sinx)

= sinx

So the derivative of 1 minus cosx is equal to sinx.

ALSO READ:

Derivative of 1/sinx: The derivative of 1/sinx is -cosecx cotx.

Derivative of $\dfrac{1}{\sqrt[3]{x}}$: The derivative of $\dfrac{1}{\sqrt[3]{x}}$ is $-\dfrac{1}{3\sqrt[3]{x^4}}$.

Derivative of sin2x: The derivative of sin2x is 2sinx cosx.

Derivative of 1/logx: The derivative of 1/logx is -1/x(log x)2.

FAQs