General Solution of tanx=tany | tanθ=tanα General Solution

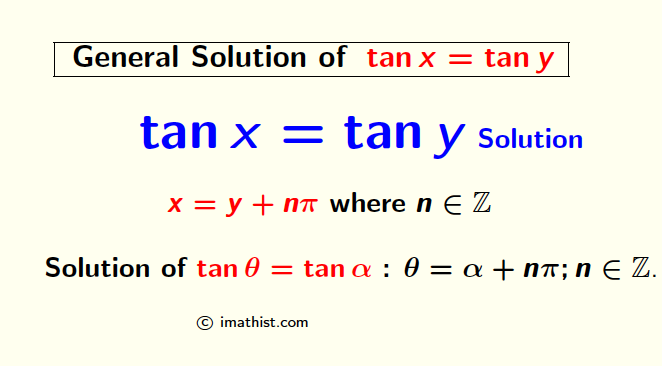
The general solution of tanx=tany for x is given by x=nπ+y where n= 0, ±1, ±2, ±3, …. In this post, we will learn how to find the general solution of tanx=tany as well as tanθ=tanα.

Solutions of tanx = tany are given by x=nπ+y, n ∈ ℤ

Let us now solve the trigonometric equation tanx = tany.

tanx=tany General Solution

To find the general solution of tanx=tany, we will follow the below steps:

Step1: Using tanx=sinx/cosy, we can write the original equation as follows.

tanx=tany

⇒ $\dfrac{\sin x}{\cos x} = \dfrac{\sin y}{\cos y}$

⇒ $\dfrac{\sin x}{\cos x} – \dfrac{\sin y}{\cos y}=0$

Step2: Cross multiplying, we will get that

$\dfrac{\sin x \cos y -\cos x \sin y}{\cos x \cos y}=0$

Step3: Let us now apply the formula sin(x-y)=sinx cosy – cosx siny. By doing so, we have that

$\dfrac{\sin (x- y)}{\cos x \cos y}=0$

⇒ sin(x-y) = 0.

⇒ x-y = nπ as we know that the general solution of sinx=0 is x=nπ for some integer n.

⇒ x = nπ+y.

So the general solution of tanx=tany is equal to x=nπ+y where n=0, ±1, ±2, ±3, ….

General Solution of tanθ=tanα

From the above, we know that the general solution of tanx=tany is

x=nπ+y.

Substituting x=θ and y=α, we will get the general solution of tanθ=tanα which is equal to θ=nπ+α where n is an integer.

ALSO READ:

• General solution of sinx=0, cosx=0, tanx=0
• Values of sin15, cos15, tan15
• Values of sin75, cos75, tan75

FAQs