If y=cos(x+y) then Find dy/dx [Solved]

If y=cos(x+y), then dy/dx= -sin(x+y)/[1+sin(x+y)]. Here, we learn how to differentiate y=cos(x+y) with respect to x. Let us find the derivative of y=cos(x+y).

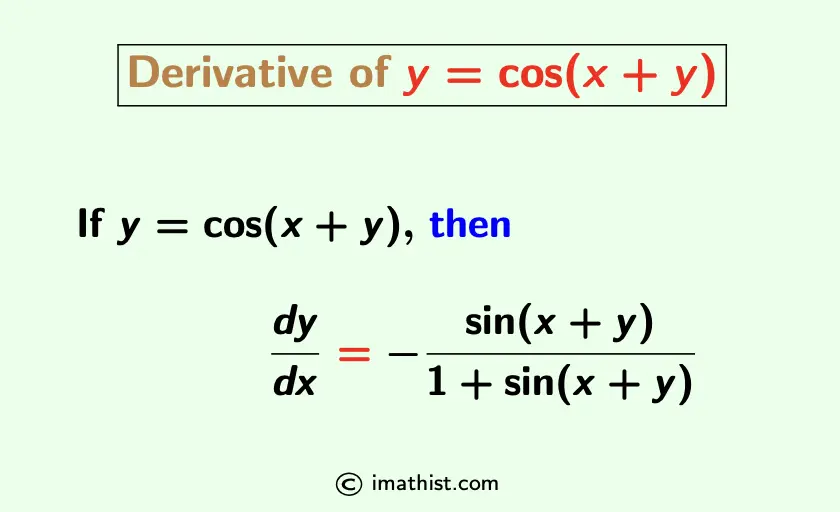
Find dy/dx if y=cos(x+y)

Question: If y=cos(x+y), then $\dfrac{dy}{dx}$.

Solution:

We are given that

y = cos(x+y).

Step 1: Differentiating both sides of the above equation with respect x, we get that

$\dfrac{dy}{dx}$ = $-\sin(x+y)\dfrac{d}{dx}(x+y)$, by the chain rule.

⇒ $\dfrac{dy}{dx}$ = $-\sin(x+y)(1+\dfrac{dy}{dx})$

Step 2: We now solve the above equation for dy/dx.

$\dfrac{dy}{dx}$ = $-\sin(x+y)-\sin(x+y)\dfrac{dy}{dx}$

⇒ $\dfrac{dy}{dx} + \sin(x+y)\dfrac{dy}{dx}$ = $-\sin(x+y)$

⇒ $[1+\sin(x+y)]\dfrac{dy}{dx}$ = $-\sin(x+y)$

⇒ $\dfrac{dy}{dx} = -\dfrac{\sin(x+y)}{1+\sin(x+y)}$.

Therefore, if y=cos(x+y), then dy/dx= -sin(x+y)/[1+sin(x+y)].

Related Questions:

If y=sin(x+y) then Find dy/dx

Derivative of $\dfrac{1}{\sin x}$

Derivative of $\dfrac{\sin x}{x}$

Derivative of $\sqrt{\sin x}$

FAQs