If y=sin(x+y) then Find dy/dx [Solved]

If y=sin(x+y), then dy/dx= cos(x+y)/[1-cos(x+y)]. Here, we learn how to differentiate y=sin(x+y) with respect to x. Let us find the derivative of y=sin(x+y).

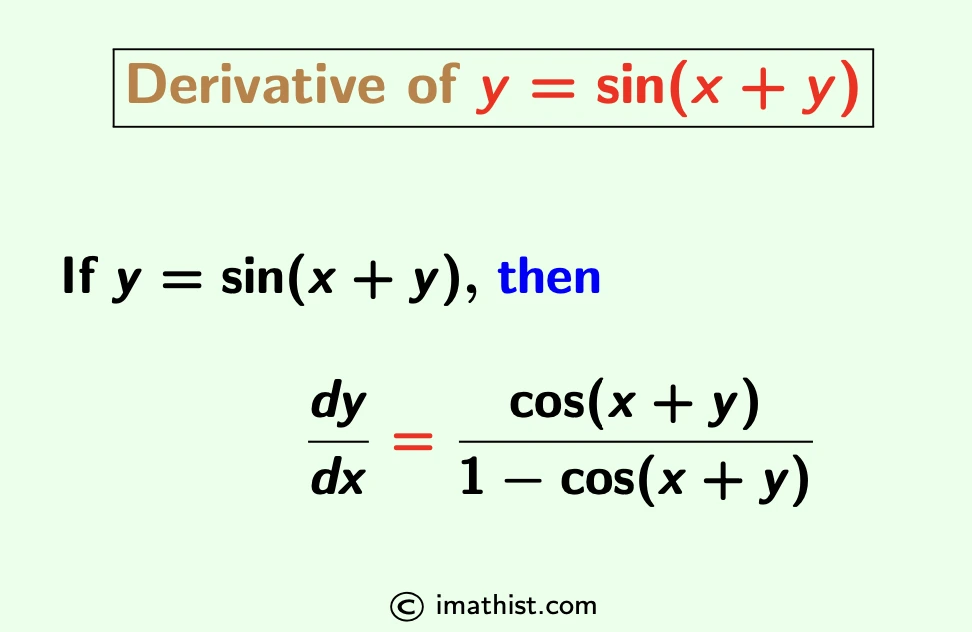
y=sin(x+y), Find dy/dx

Question: If y=sin(x+y), then $\dfrac{dy}{dx}$.

Solution:

Given, y = sin(x+y).

To find dy/dx, we will differentiate both sides of the equation y=sin(x+y) with respect x. Using the chain rule, we get that

$\dfrac{dy}{dx}$ = $\cos(x+y)\dfrac{d}{dx}(x+y)$

⇒ $\dfrac{dy}{dx}$ = $\cos(x+y)(1+\dfrac{dy}{dx})$

Solving the above equation for dy/dx, it follows that

$\dfrac{dy}{dx}$ = $\cos(x+y)+\cos(x+y)\dfrac{dy}{dx}$

⇒ $\dfrac{dy}{dx} – \cos(x+y)\dfrac{dy}{dx}$ = $\cos(x+y)$

⇒ $[1-\cos(x+y)]\dfrac{dy}{dx}$ = $\cos(x+y)$

⇒ $\dfrac{dy}{dx} = \dfrac{\cos(x+y)}{1-\cos(x+y)}$.

So we conclude that if y=sin(x+y), then dy/dx= cos(x+y)/[1-cos(x+y)].

Related Questions:

Derivative of 1/sinx

Derivative of sinx/x

What is the derivative of root sin x

FAQs