Integral of cosec square x | Cosec^2x Integration

The integral of cosec square x is equal to -cot(x)+C where C is a constant. In this post, we will learn how to integrate cosec^2x.

The integration formula of cosec^2x is given as follows:

∫cosec²x dx = -cotx+C

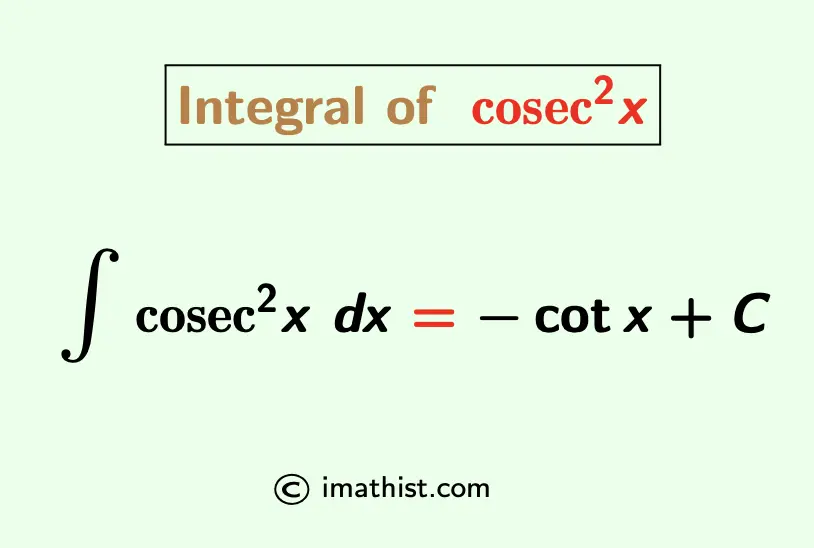
What is the Integration of cosec^2x

Answer: The integration of cosec²x is -cotx+C.

Proof:

First, recall the function whose derivative is the function cosec²x. We know that the derivative of cotx is equal to -cosec²x, and so we have that

$\dfrac{d}{dx}$(-cot x) = cosec²x.

Now, we integrate both sides. As a result, we get that

∫$\dfrac{d}{dx}$(-cot x) = ∫cosec²x dx +c, c is an integral constant.

⇒ -cotx = ∫cosec²x dx +c, by the fact: integration is the opposite process of derivatives.

⇒ ∫cosec²x dx = -cotx -c

⇒ ∫cosec²x dx = -cotx +C where C= -c.

So the integration of cosec²x (cosec square x) is equal to -cotx+C where C denotes an integral constant.

Read These Derivatives:

Integration of sin2x	Integration of cos2x
Integration of tan2x	Integration of cot2x

FAQs