Integral of sin root x dx | Find ∫sin(√x)dx

The integral of sin root x dx is denoted by ∫sin(√x)dx, and it is given by ∫sin(√x)dx = 2[-√xcos(√x)+ sin(√x)]+C where C denotes an integral constant.

Note that

$\int \sin \sqrt{x} dx$ $= 2[-\sqrt{x} \cos \sqrt{x}+\sin \sqrt{x}]+C$

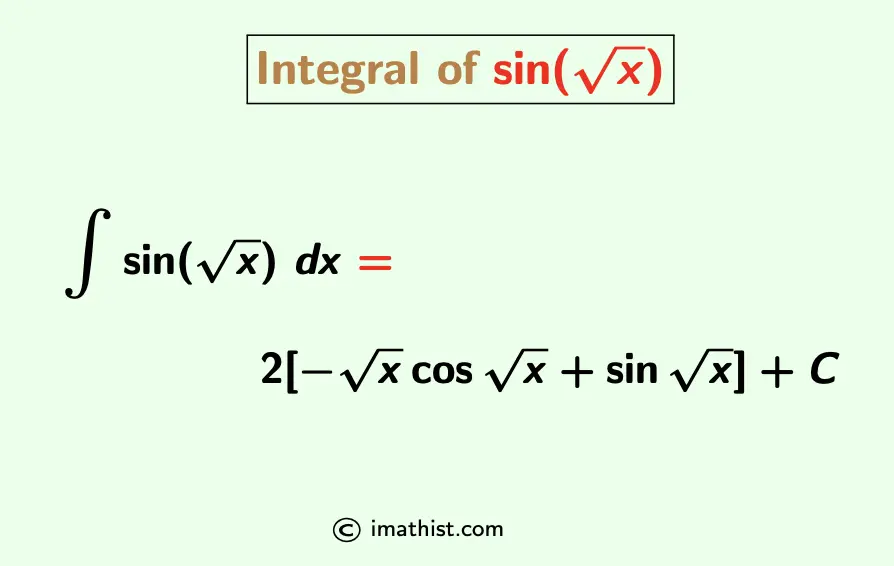
Lets learn how to integrate sin(sqrt x) dx.

Integration of sin root x

Question: Find the integral ∫sin(√x)dx.

Answer:

Let I = ∫sin(√x)dx.

Put √x=t, that is, x=t².

So dx = 2tdt

Now, I = ∫sin(√x)dx = 2 ∫tsin(t) dt

Now integrating by parts formula: ∫uv dx = u ∫v dx – ∫[$\frac{du}{dx}$∫v dx] dx (where u, v are functions of x) with

u= t, v=sint

we get that

I = 2 ∫tsin(t) dt

= 2 [t ∫sint dt – ∫{$\frac{dt}{dt}$∫sint dt} dt ] + C

= 2[-t cost + ∫cost dt] + C

= 2[-t cost + sint] + C

= 2[-√x cos(√x) + sin(√x)] + C.

So the integral of sin(sqrt x) is equal to ∫sin(√x)dx = 2[-√x cos(√x) + sin(√x)] + C where C is an arbitrary integration constant.

More Integrals:

Integral of square root of tanx

Integral of sin³x

Integral of log(sin x)

Integration of root tanx + root cotx

FAQs