How to Integrate 1/(1+x^2) | Integration of 1/(1+x^2)

The integration of 1/(1+x²) is tan^-1x+C. In this post, we will learn how to integrate 1 divided by 1 plus x square by the substitution method.

Integration of 1/(1+x²) Formula

1/(1+x²) integral formula: The integration formula of 1/(1+x^2) is provided below.

∫ 1/(1+x²) dx = tan^-1x+C.

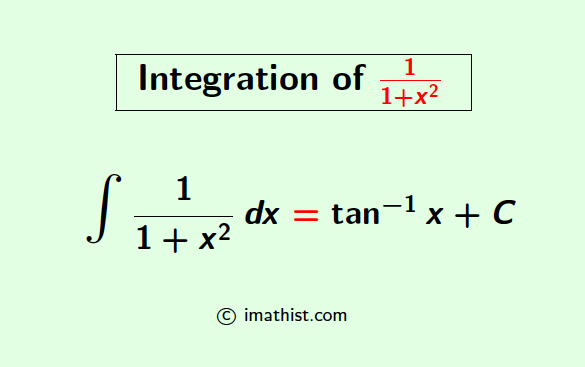
Integration of 1/(1+x²) Proof

Now, we will prove that

∫1/(1+x2) dx = tan-1x+C.

Let x=tanθ

Differentiating both sides using the fact d(tanθ)/dθ = sec²θ, we get that

dx = sec²θ dθ

Therefore, ∫1/(1+x²) dx = ∫sec²θ/(1+tan²θ) dθ

= ∫sec²θ/sec²θ dθ using the trigonometric identity 1+tan²θ=sec²θ

= ∫dθ

= θ+C

= tan^-1x+C as x=tanθ.

So the integration of 1/(1+x²) is tan^-1x+C where C is an integral constant. This is obtained by the substitution method where we put x=tanθ.

Video Solution on Integration of 1/(1+x²) dx:

ALSO READ:

Integration of tan x : The integration of tanx is sec²x.

Integration of cot x : The integration of cotx is -cosec²x.

Integration of sec x : The integration of secx is log_e|secx+tanx|.

Integration of cosec x : The integration of cosecx is log_e|cosecx-cotx|.

FAQs