Integration of root 1+sin2x | ∫√(1+sin2x) dx

The integration of the square root of 1+sin2x is given by

∫√(1+sin2x) dx = cosx-sinx+C

where C is an integration constant. In this post, we will learn how to integrate square root of 1+sin2x.

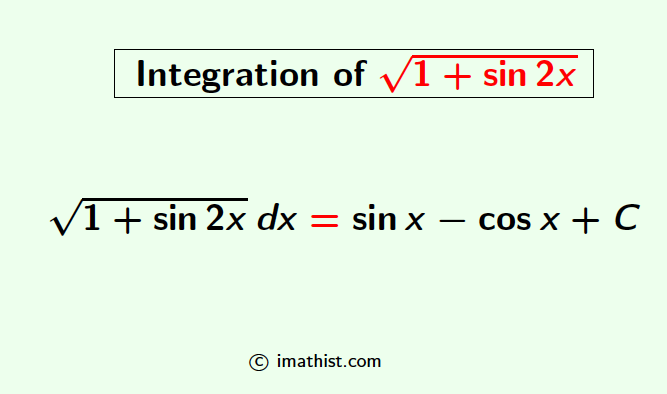
Integral of Square Root of 1+sin2x

Question: Find the integral of 1+sin2x, that is, find

∫√(1+sin2x) dx.

Answer:

We will use the following two trigonometric formulas:

1. sin²x+cos²x = 1
2. sin2x= 2sinxcosx

By the above two formulas, we have that

1+sin2x = sin²x+cos²x+2sinxcosx = (sinx+cosx)²

Taking square root of both sides, we obtain that

√(1+sin2x) = sinx+cosx

Integrating both sides, we get that

∫√(1+sin2x) dx = ∫(sinx+cosx) dx + C, C is an integral constant.

= ∫sinx dx + ∫cosx dx + C

= -cosx+sinx+C.

So the integration of square root of 1+sin2x is equal to -cosx+sinx+C where C is an integration constant.

Integration of root 1+sin2x from 0 to pi/2

Question: Find the integral of root 1+sin2x from 0 to π/2.

Answer:

From above, we have ∫√(1+sin2x) dx = cosx-sinx+C. Thus, the definite integral of root 1+sin2x from 0 to π/2 will be equal to

$\int_0^{\pi/2} \sqrt{1+\sin 2x} dx$

= $[\cos x -\sin x]_0^{\pi/2}$

= (cos π/2 – sin π/2) – (cos0 – sin0)

= (0-1) – (1-0)

= -1-1

= -2

So the integration of root 1+sin2x from 0 to pi/2 is equal to -2.

ALSO READ:

Integration of log(sinx) from 0 to pi/2

Integration of root x

Integration of cube root x

Integration of root(x)+1/root(x)

FAQs