Integration of root tanx + root cotx | Find ∫(√tanx+√cotx) dx

The integration of root tanx + root cotx is equal to √2sin^-1(sinx−cosx)+C. Here we learn how to integrate √tanx+√cotx.

The integral formula of $\sqrt{\tan x}+\sqrt{\cot x}$ is given by

$\int (\sqrt{\tan x}+\sqrt{\cot x}) dx$ = $\sqrt{2}\sin^{-1}(\sin x -\cos x)+C$.

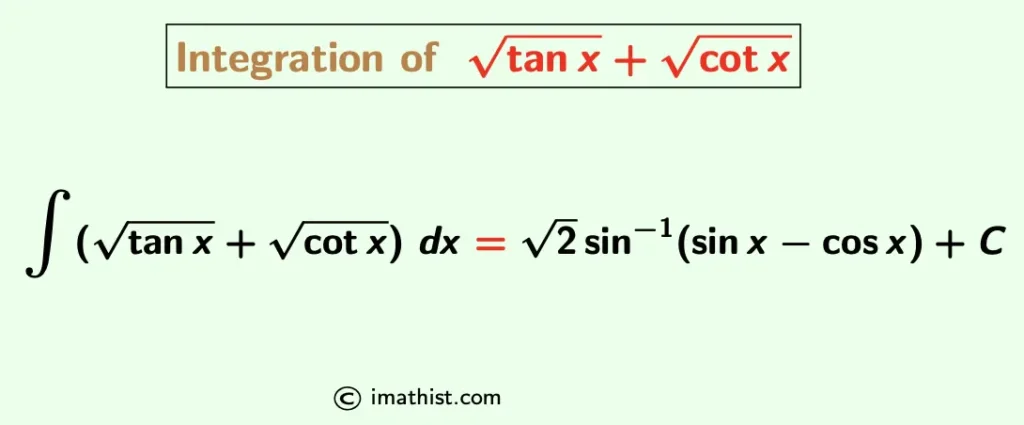
Find ∫(√tanx+√cotx) dx

$\int (\sqrt{\tan x}+\sqrt{\cot x}) dx$

= $\int \Big(\dfrac{\sqrt{\sin x}}{\sqrt{\cos x}}+\dfrac{\sqrt{\cos x}}{\sqrt{\sin x}} \Big) dx$

= $\int \dfrac{\sin x + \cos x}{\sqrt{\sin x} \sqrt{\cos x}} dx$

= $\sqrt{2} \int \dfrac{\sin x + \cos x}{\sqrt{2\sin x \cos x}} dx$

= $\sqrt{2} \int \dfrac{\sin x + \cos x}{\sqrt{2\sin x \cos x+1-\sin^2x-\cos^2x}} dx$ as we know sin²x+cos²x=1.

= $\sqrt{2} \int \dfrac{\sin x + \cos x}{\sqrt{1-(\sin x -\cos x)^2}} dx$

[ Put sinx -cosx =t, so that (cosx +sinx)dx =dt ]

= $\sqrt{2} \int \dfrac{dt}{\sqrt{1-t^2}}$

= $\sqrt{2} \sin^{-1}t+C$

= $\sqrt{2} \sin^{-1}(\sin x -\cos x)+C$

So the integral of root(tanx) + root(cotx) is equal to √2sin^-1(sinx−cosx)+C, where C is an integral constant.

More Integrals:

Find ∫√tanx dx | Find ∫lnx dx

Find ∫log(sinx) dx | Find ∫e^2x dx

Find ∫e^3x dx

FAQs