Limit of (a^x-1)/x as x approaches 0: Formula, Proof

Answer: The limit of (ax -1)/x when x tends to 0 is equal to lna, that is, limx→0 (ax -1)/x =lna.

The limit of (a^x-1)/x as x approaches 0 is equal to 1. The lim_{x -> 0} (a^x-1)/x formula is given by

$\lim\limits_{x \to 0} \dfrac{a^x-1}{x}=\ln a$

where ln a = log_ea. In this post, we will learn to prove the limit of (a^x-1)/x when x tends to zero.

Table of Contents

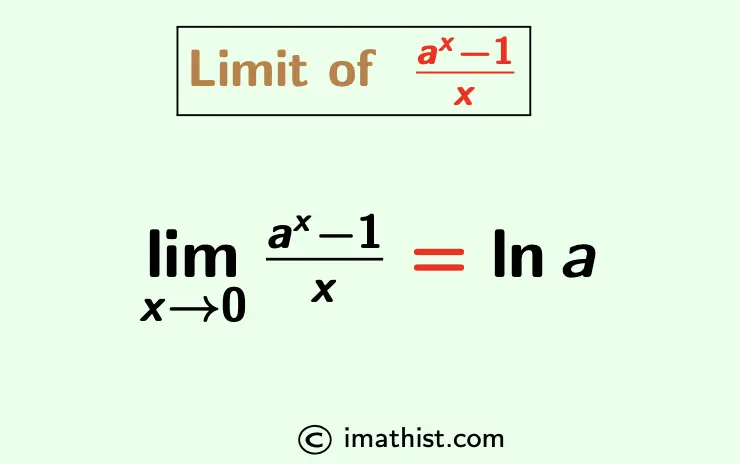
Lim_{x → 0} (a^x -1)/x

Prove that lim_{x → 0} (a^x -1)/x = ln a.

Answer:

As a^x= e^{x lna}, the given limit lim_{x → 0} (a^x -1)/x can be written as follows.

$\lim\limits_{x \to 0} \dfrac{e^{x \ln a}-1}{x}$

= $\ln a \lim\limits_{x \to 0} \dfrac{e^{x \ln a}-1}{x\ln a}$

[ Let xlna =t. Then t→0 when x→0 ]

= $\ln a \lim\limits_{t \to 0} \dfrac{e^{t}-1}{t}$

= $\ln a \times 1$ by the limit formula lim_x→0 (e^x-1)/x = 1.

= ln a

So the limit of (a^x -1)/x is equal to lna when x→0.

More Limits:

Answer: The limit of (a^x -1)/x when x tends to 0 is equal to lna, that is, lim_x→0 (a^x -1)/x =lna.

Spread the love