Limit of cos(1/x) as x approaches infinity

Answer: The limit of cos(1/x) is equal to 1 when x tends to ∞, that is, limx→∞ cos(1/x) =1.

The limit of cos(1/x) as x approaches infinity is equal to 1. The lim_x→∞ cos(1/x) formula is given as follows:

$\lim\limits_{x \to \infty} \cos \big(\dfrac{1}{x} \big)=1$.

In this post, we will learn how to prove the limit of cos(1/x) when x tends to ∞.

Table of Contents

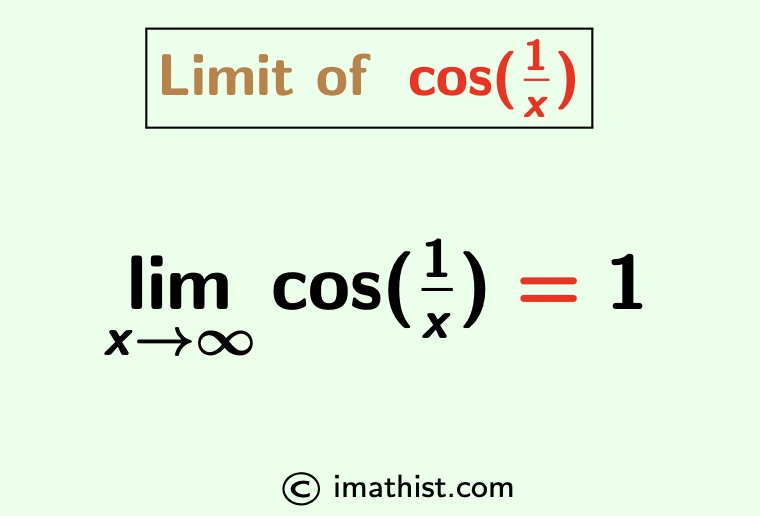
Lim_x→∞ cos(1/x)

Question: What is the limit of cos(1/x) when x tends to infinity?

Answer: The limit of cos(1/x) is equal to 1 when x tends to infinity.

Explanation:

Put $z=\dfrac{1}{x}$.

So z→0 when x→∞.

∴ The given limit

$\lim\limits_{x \to \infty} \cos \big(\dfrac{1}{x} \big)$

= $\lim\limits_{z \to 0} \cos z$

= $\cos 0$

= 1.

So the limit of cos(1/x) is equal to 1 when x→∞.

Read Also: Limit of sin(1/x) when x→0

Have You Read These Limits?

lim_x→0 sin(√x)/x	lim_x→0 sin(x²)/x
lim_x→∞ sinx/x	lim_x→0 x/sinx

Answer: The limit of cos(1/x)is equal to 1 when x tends to ∞, that is, lim_x→∞ cos(1/x) =1.

Spread the love