Limit of (cosx-1)/x as x approaches 0

The limit of (cosx-1)/x as x approaches 0 is equal to 0. Here, we will learn to find the limit of (cos(x)-1)/x when x→0. The limit formula of (cosx-1)/x as x tends to 0 is given by

lim_x→0 $\dfrac{\cos x -1}{x}$ = 0.

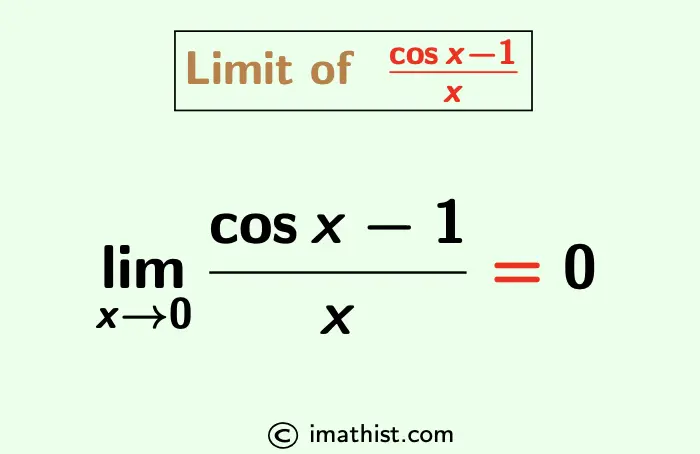
Proof of Limit of (cosx-1)/x as x approaches 0

Prove that lim_x→0 $\dfrac{\cos x -1}{x}$ = 0.

Proof:

The following steps have to be followed in order to find the limit of cos(x)-1 divided by x as x approaches zero.

Step 1: Multiply both the numerator and the denominator of (cosx-1)/x by cosx+1. Thus, we obtain that

lim_x→0 $\dfrac{\cos x -1}{x}$ = lim_x→0 $\dfrac{(\cos x -1)(\cos x +1)}{x(\cos x +1)}$

= lim_x→0 $\dfrac{\cos^2 x -1}{x(\cos x +1)}$ by the formula (a-b)(a+b) = a²-b².

Step 2: Applying the formula sin²x+cos²x=1, that is, cos²x -1 = -sin²x, the above limit will be equal to

= lim_x→0 $\dfrac{-\sin^2 x}{x(\cos x +1)}$

= – lim_x→0 $\dfrac{\sin x}{x}$ × lim_x→0 $\dfrac{\sin x}{\cos x +1}$ by the product rule of limits.

= -1 × $\dfrac{\sin 0}{\cos 0 +1}$as the limit of sinx/x is equal to 1 when x tends to 0.

= $-\dfrac{0}{1 +1}$

= 0.

So the value of the limit of (cosx-1)/x as x approaches 0 is equal to 0.

ALSO READ:

limx→∞ sinx/x = 0	limx→0 x/sinx = 1
limx→∞ cos(1/x) = 0	limx→0 sin(1/x) = undefined

Proof of lim_x→0 (cosx -1)/x = 0 by L’Hôpital’s rule

Let us now prove that the limit of (c0s(x)-1)/x as x approaches to 0 is equal to 0 by L’Hôpital’s rule. See that

(c0s0-1)/0 = (1-1)/0 = 0/0, so it is an intermediate form. Hence using the L’Hôpital’s rule, we get that

lim_x→0 $\dfrac{\cos x -1}{x}$

= lim_x→0 $\dfrac{\frac{d}{dx}(\cos x -1)}{\frac{d}{dx}(x)}$

= lim_x→0 $\dfrac{-\sin x}{1}$

= -sin0/1

= 0/1 as the value of sin0 is 0.

= 0.

Thus the limit of (cosx-1)/x when x approaches to 0 is equal to zero, and this is obtained by the L’Hôpital’s rule.

Have You Read These Limits?

limx→0 x/cosx = 0	limx→0 tanx/x = 1
limx→0 (ex-1)/x = 1	limx→∞ tanx/x = undefined

FAQs