The simplification of the expression 1-sec2x is equal to -tan2x. In this post, we will establish 1-sec^2x formula.
We have:
- 1- sec2x = – tan2x
- 1- sec2θ = – tan2θ.
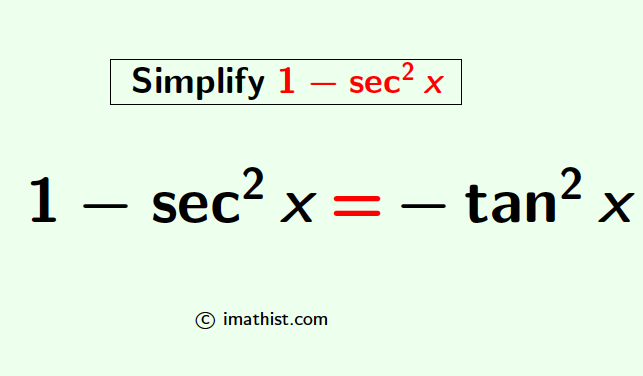
Let us now prove the above formulas.
1-sec2x Formula
The formula of 1-sec2x is given below:
$\boxed{1-\sec^2 x=-\tan^2 x}$
Proof:
To simplify the expression $1-\sec^2 x$, we will follow the below steps:
Step 1: We will use the following trigonometric identities to find the value of 1-sec2x:
- sin2x +cos2x = 1
- secx = 1/cosx
- tanx = sinx/cosx
Step 2: Substituting the value of secx from the above in the expression 1-sec2x, we will get that
1-sec2x = $1-\left(\dfrac{1}{\cos x} \right)^2$
= $1-\dfrac{1}{\cos^2 x}$
= $\dfrac{\cos^2 x -1}{\cos^2 x}$
= $\dfrac{\cos^2 x -(\sin^2 x +\cos^2 x)}{\cos^2 x}$
= $\dfrac{\cos^2 x -\sin^2 x -\cos^2 x}{\cos^2 x}$
= $\dfrac{-\sin^2 x}{\cos^2 x}$
= $- \left(\dfrac{\sin x}{\cos x} \right)^2$
= – tan2x
Thus, the simplification or the formula of 1-sec2x is equal to – tan2x.
Remark: Putting x=θ in the above formula, we get the following simplification of 1-sec2θ:
1-sec2θ = – tan2θ.
Also Read:
Question-Answer on 1-sec2x Formula
Question 1: Find the value of 1-sec245°
Answer:
From the above, we know that
1-sec2θ = – tan2θ
Put θ = 45°.
So we get that
1-sec245° = – tan245°
= -12 as we know that tan45°=1.
= -1
So the value of 1-sec245° is equal to -1.
FAQs
Q1: What is the formula of 1-sec2x?
Answer: The formula of 1-sec2x is given by 1-sec2x= -tan2x.
Q2: What is the formula of 1-sec2θ?
Answer: The formula of 1-sec2θ is given as follows: 1-sec2θ= -tan2θ.