Sin Cube x Formula, Proof | Sin^3x Formula

The sin cube x formula is given as follows: sin³x = (3sinx -sin3x)/4, that is, sin^3x formula is equal to (3sinx – sin3x) divided by 4. Here we establish the formula of sine cube x and give a proof.

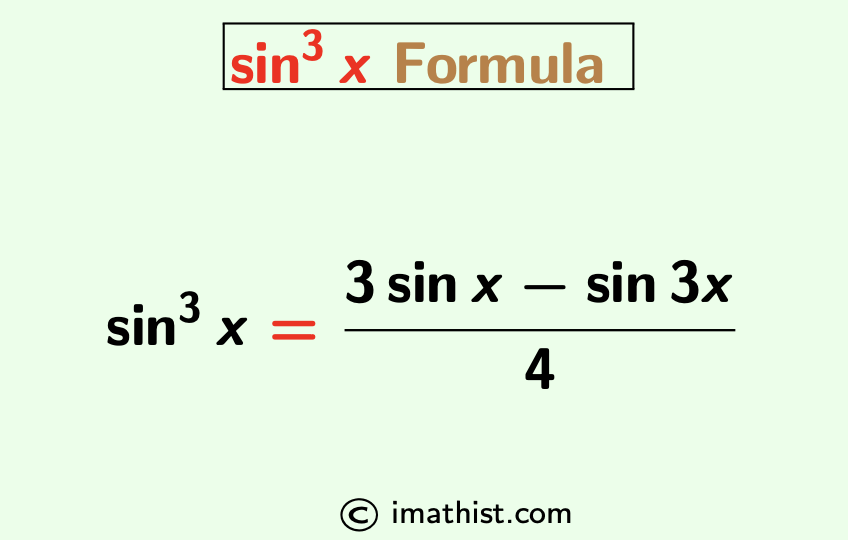
What is sin cube x formula

Answer: sin³x = (3sinx -sin3x)/4

Proof:

To establish the formula of sin^3x, we will use sin3x formula which is provided below:

sin3x = 3sinx – 4sin³x.

Adding -3sinx to both sides, we get that

– 3sinx + sin3x = – 3sinx + 3sinx – 4sin³x

⇒ – 3sinx + sin3x = – 4sin³x

⇒ 3sinx – sin3x = 4sin³x (changing the signs)

Dividing both sides, we obtain that

(3sinx – sin3x)/4 = sin³x.

So the sin³x formula is given by sin³x = (3sinx – sin3x)/4 and this is proved by using the formula of sin3x.

Have You Read These? 

Sin3x Formula	Cos3x Formula
Tan2x Formula	Simplify cos(sin-1x)
Simplify sin(cos-1x)	cos2x-sin2x Formula

Integration of sin^3x Formula

Using the above sin³x formula sin³x = (3sinx -sin3x)/4, the integration of sin^3x will be calculated as follows.

∫sin3x dx = ∫ (3sinx -sin3x)/4 dx ⇒ ∫sin3x dx = 3/4 ∫sinx dx – 1/4 ∫sin3x dx ⇒ ∫sin3x dx = – 3/4 cosx + 1/4 (cos3x)/3 + C as the integral of sin(mx) is equal to -cos(mx)/m. ⇒ ∫sin3x dx = – (3cosx)/4 + (cos3x)/12 + C.

So the integration of sin cube x is equal to ∫sin³x dx = – (3cosx)/4 + (cos3x)/12 + C where C is an integral constant.

Derivative of sin^3x Formula

The derivative of sin^3x is calculated as given below.

$\dfrac{d}{dx}(\sin^3 x)$ = $3\sin^2 x \cdot \dfrac{d}{dx}(\sin x)$ = $-3\sin^2 x \cos x$.

So the derivative of sine cube x with respect to x is equal to -3sin²x cosx, that is, d/dx(sin³x) = -3sin²x cosx.

FAQs