sin(pi/2-x) Formula | Simplify sin(x-π/2)

The sin(π/2-x) formula is given as follows:

sin(π/2-x)=cosx …(∗)

The formula of sin(pi/2-θ) is given by sin(π/2-θ)=cosθ. In this post, we will learn how to compute sin(pi/2-x) or sin(θ-pi/2).

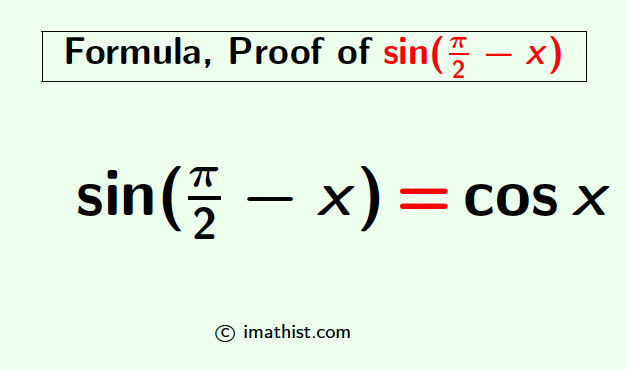
Proof of sin(pi/2-x) Formula

To establish the above formula (∗), that is, the formula of sin(π/2-x), we need to apply the below formula:

sin(a-b) = sina cosb – cosa sinb …(∗∗)

Put a=π/2, b=x. Thus, we get that

sin(π/2-x) = sin(π/2) cosx – cos(π/2) sinx

= 1⋅cosx – 0⋅sinx as we know that sin(π/2)=1 and cos(π/2)=0.

= cosx – 0

= cosx

So we have proved the formula of sin(π/2-x) which is given below:

sin(π/2-x) = cosx

In the above formula, if we replace x by θ, we will get the formula of sin(π/2-θ) which is provided below:

sin(π/2-θ) = cosθ

Proof of sin(x-pi/2) Formula

In the above formula (∗) of sin(a-b), we put

a=x, b=π/2.

Thus, sin(x-π/2)

= sinx cos(π/2) – cosx sin(π/2)

= sinx ⋅ 0 – cosx ⋅ 1

= -cosx

So the formula of sin(x-π/2) is equal to sin(x-π/2)=-cosx.

Similarly, the formula of sin(theta-π/2) is equal to sin(θ-π/2)=-cosθ.

Also Read:

Simplify cos(π-x)

Simplify cos(sin-1x)

sin(π-x) Formula

1+cot2x Formula

FAQs