sinx cosy Formula | sinx cosy Identity

The formula or the identity of the product sinx cosy is obtained by the transformation of sums or differences of trigonometric angles. sinx cosy formula is given below.

sinx cosy = $\dfrac{\sin(x+y)+\sin(x-y)}{2}$

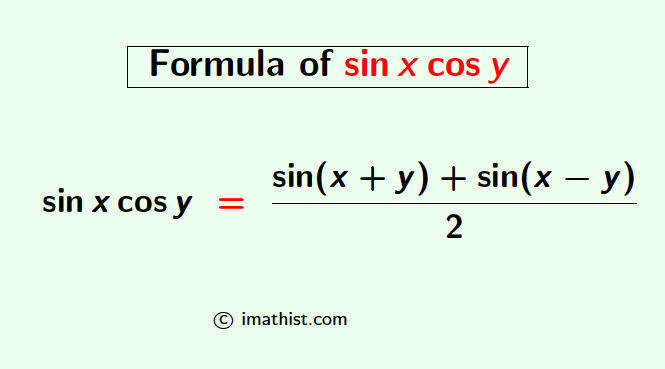
Proof of sinx cosy Formula

Let us now prove the sinx siny formula

sinx cosy = $\dfrac{\sin(x+y)+\sin(x-y)}{2}$

Proof:

It is known that

sin(x+y) = sinx cosy + cosx siny …(I)

sin(x-y) = sinx cosy – cosx siny …(II)

Adding (I) and (II), we obtain that

sin(x+y) + sin(x-y) = (sinx cosy + cosx siny) + (sinx cosy – cosx siny)

⇒ sin(x+y) + sin(x-y) = sinx cosy + cosx siny + sinx cosy – cosx siny

⇒ sin(x+y) + sin(x-y) = 2sinx cosy

Dividing both sides by 2, we get that

sinx cosy = $\dfrac{\sin(x+y)+\sin(x-y)}{2}$

So the formula of sinx cosy formula is given as follows: sinx cosy= 1/2 [sin(x+y) + sin(x-y)].

sinx cosy Formula:

$\sin x \cos y = \dfrac{\sin(x+y)+\sin(x-y)}{2}$

ALSO READ:

sinx siny Formula

cosx cosy Formula

cosx siny Formula

Application of sinx cosy Formula

Question 1: Find the value of sin45 cos15.

Answer:

By the above formula with x=45 and y=15, we will obtain that

sin45 cos15 = $\dfrac{\sin(45+15)+\sin(45-15)}{2}$

= $\dfrac{\sin 60+\sin 30}{2}$

= $\dfrac{\frac{\sqrt{3}}{2} +\frac{1}{2}}{2}$

= $\dfrac{\frac{\sqrt{3}+1}{2}}{2}$

= $\dfrac{\sqrt{3}+1}{4}$

Thus, the value of sin45 cos15 is equal to (√3+1)/4.

FAQs