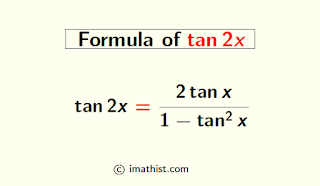Tan2x Formula in terms of Tanx, Sinx, Cosx [with Proof]

Tan2x formula in terms of tanx is as follows: $\dfrac{2\tan x}{1-\tan^2x}$. Here, we will also derive the tan2x formula in terms of sinx and cosx along with some examples. These formulas are very useful to solve trigonometric equations and simplify trigonometric expressions.

Tan2x Formula

Tan2x is the tangent function of a double angle 2x. The formula of tan2x in terms of tanx is given as follows.

$\tan 2x=\dfrac{2\tan x}{1-\tan^2x}$.

Tan2x in Terms of Tanx

To derive the tan 2x formula, we will use the trigonometric formula below:

$\tan(a+b)$ $=\dfrac{\tan a +\tan b}{1-\tan a\tan b}$

At first, we will write 2x as x+x, and then we will apply the above formula. By doing so, we get that

$\tan 2x=\tan(x+x)$

$=\dfrac{\tan x+\tan x}{1-\tan x \tan x}$

$=\dfrac{2\tan x}{1-\tan^2x}$

Tan2x Formula Proof

Now, we will prove the tan2x formula using sin2x and cos2x formulas which are given below.

1. $\tan x=\dfrac{\sin x}{\cos x}$
2. $\sin 2x =2\sin x\cos x$
3. $\cos 2x=\cos^2x-\sin^2x$

Then we have $\tan 2x =\dfrac{\sin 2x}{\cos 2x}$

$=\dfrac{2\sin x \cos x}{\cos^2x-\sin^2x}$

Dividing both the numerator and denominator by $\cos^2x$, we get that

$\tan 2x=\dfrac{\dfrac{2\sin x \cos x}{\cos^2x}}{\dfrac{\cos^2x-\sin^2x}{\cos^2x}}$

$=\dfrac{2\dfrac{\sin x}{\cos x} cdot \dfrac{\cos x}{\cos x}}{\dfrac{\cos^2x}{\cos^2x}-\dfrac{\sin^2x}{\cos^2x}}$

$=\dfrac{2\tan x}{1-\tan^2x}$

Thus, we have proved the formula of tan2x which is $\dfrac{2\tan x}{1-\tan^2x}$.

Tan2x in Terms of Sinx

Now we will derive the tan2x formula, in terms of sinx. In order to do so, we will go through the following way:

$\tan 2x=\dfrac{\sin 2x}{\cos 2x}$

$=\dfrac{2\sin x \cos x}{1-2\sin^2x}$ as cos2x=1-2sin²x

$=\dfrac{2\sin x}{1-2\sin^2x} \sqrt{1-\sin^2x}$ as cos²x=1-sin²x

Tan2x in Terms of Cosx

Now we will derive the tan2x formula, in terms of cosx. In order to do so, we will go through the following way:

$\tan 2x=\dfrac{\sin 2x}{\cos 2x}$

$=\dfrac{2\sin x \cos x}{2\cos^2x-1}$ as $\cos 2x=2\cos^2x-1$

$=\dfrac{2\cos x}{2\cos^2x-1} \sqrt{1-\cos^2x}$ as $\sin^2x=1-\cos^2x$

Also Read:

Simplify 1-sin²x

sin3x Formula in terms of sinx

Values of sin15, cos15, tan15

Values of sin75, cos75, tan75

Simplify cos(sin^-1x)

Simplify sin(cos^-1x)

Question: Find the Value of $\tan 120^\circ$.

Answer:

We have from the above that $\tan 2x=\dfrac{2\tan x}{1-\tan^2x}$.

Put $x=60^\circ$

Then $\tan 120^\circ=\dfrac{2\tan 60^\circ}{1-\tan^2 60^\circ}$

$=\dfrac{2\tan 60^\circ}{1-\tan^2 60^\circ}$ as $\tan 60^\circ=\sqrt{3}$

$=\dfrac{2\sqrt{3}}{1-(\sqrt{3})^2}$

$=\dfrac{2\sqrt{3}}{1-3}$

$=-\sqrt{3}$.

So the value of tan120 degrees is equal to root 3.

FAQs