Answer: The Laplace transform of 0 is equal to L{0} = 0.
In this post, we learn to find the Laplace of zero. The formula of the Laplace transform of zero is given as follows:
| L{0} = 0. |
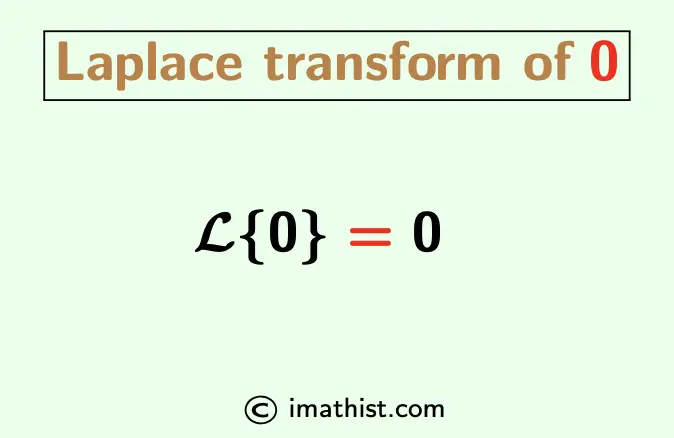
Laplace Transform of 0
By definition, the Laplace of f(t) is given by the integral
L{f(t)} = $\int_0^\infty$ e-st f(t) dt
Let f(t) = 0.
∴ L{0} = $\int_0^\infty$ (0 ⋅ e-st) dt
= = $\int_0^\infty$ 0 dt
= 0
So the Laplace transform of 0 (zero) is 0.
Note: We know that the Laplace of a constant c is equal to c/s, so the Laplace of 0 will be equal to 0/s =0.
Related Topics:
FAQs
Q1: What is the Laplace transform of 0 (zero)?
Answer: The Laplace transform of zero is equal to 0.
Q2: Find L{0}.
Answer: L{0} = 0.